What do you mean by combo mod? What would it do?Squishykorean wrote:
Has anyone talked about combo as being a mod?
Just like how perfect and sudden death are mods, combo is pretty much just the more lenient form of sudden death where you don't die when you combo break. It could give like a score multiplier or something so people have an incentive to use it.
So on a song that is really hard to FC because of some dense minijack or burst that only a few people can get will be much more rewarding for those who can FC and won't be discouraged if their full combo was beaten by some better accuracy player that completely missed that one impossible section.
This would make it more appealing for tourneys as missing a note midway basically ruins your potential from scoring an even remotely decent score while getting a full combo will be very rewarding.
show more
Accuracy score should be the main value used for the rest of the performance and ranking system (as long there is only one ranking based on the one-dimensional pp value of each player), since the count of the judgments is a more reliable statistic to base inferences about the skill of a player, compared to the length of string of non-misses (mixing both by adding two different formulas together doesn't make it better than a pure accuracy-based formula either, the quality of the formula used for overall score increases the lower the weight of the combo portion of it is).
That said, basing the accuracy score on the current Accuracy Percentage formula is not good either. Accuracy Percentage underweights the importance of Rainbows over regular 300s, and overweights the importance of 200s over 100s/50s/Misses.
For measuring the ability of being able to hit hard notes without missing, miss count is a better statistic than a score based on combo.
If you want to isolate speed/dexterity skill from overall accuracy skill, ideally, you should be able to calculate 2 different scores for each aspect of skill, and have two different leaderboards and rankings for the same plays.
It sounds confusing because it's sort off tackling the same problem in the exact opposite way. You're not actually rewarding players for keeping high combos, you're just upping the punishment of misses. Fewer misses generally equal higher combo, with edge cases like FC'ing a song and then missing the last 5 notes being an exception to that rule. Unsurprisingly, these edge cases also produce funny scores in ScoreV1/V2, but not in MIGS scoring for example.
The main ways you can get a massive amount of misses and only misses is if you're very negligent in an easy section (misreads), minor misreads in hard sections (which are generally penalised less anyway) or if you're hitting extremely conservatively in hard sections. Being negligent in an easy section is usually minor (1-2 misses), it's very very rare to actually early miss a massive chord in the first place anyway. And even then, that's an extreme edge case - and an extremely rare scenario that is rarely replicated in normal gameplay and can be discarded as an anomaly in gameplay.
Combo multiplier has the issue of not being able to discriminate between 5 misses spread out in easy sections and 5 misses in a hard section, definitely, but so do misses. Having a combo multiplier is just increasing the magnitude of that source of error. This is ultimately why people don't think combo multiplier is a good idea - it's an unnecessary metric that adds nothing if the game itself does not promote the idea of "perfection". osu!mania does not promote perfection. Otherwise, the PP system would favour more towards 1mil scores rather than 700-850K scores, SR would look at only the hardest part of the chart (it technically does this already if the hard section is long enough, but it doesn't address super short spikes completely well), and non-300 judgements would be far far more punishing.
The point here is that in order to advance is not that we really need much more stuff to talk about. We saw results in the MWC4K and what we can do is just post solutions to the problem (even tho this has been done already before and we all know what happened). Hopefully those points will be used for this 7K World Cup.
It's probably only because he can't reach a high combo on that map (as you said it's "just" an A) so the shadow didn't go very low
I'm gonna ask him that personally to clear this up. Any other potential FI players you know of? I am always searching
But even if there are a few players who can play better with FI and they just don't want to, the amount is still way smaller than FL players so the point persists.
I have no feeling for score or hp values because i have too few experience with v2 so i can't give an opinion on that.
Kamikaze is a nice guy. Although our opinions almost ALWAYS differ, its nice to have him in debates like these because he brings the discussion forwards alot by always staying on topic and serving good arguments for everything. A rare ability I really appreciate.
The only reason it doesn't feel right is because you are used to the current system. Having a judgement below the highest one negatively impact accuracy makes way more sense if you get out of the old frame of mind.
edit: confusing terminology
I don't think thats the issue here. Im completely fine with all scores dropping little and S ranks becoming harder when scoreV2 goes live because i know that relatively it stays the same (I just need to get used to the new standards) but making a whole rank a once-in-a-lifetime experience is like turning it into an achievement. Imagine how the user profiles would look like, most people would have 0 SS ranks. Further more: mania is the mode with the easiest S ranks in osu!. With scoreV2 as it is it would get the hardest SS ranks which is quite a contrast.
The best way to go is how SM's new score system works, which is the system I proposed in my OD thread a while back. Have non discrete, continuous acc-score following a bell curve related to hit timing.
Ofc there is an argument about 65% FC VS 98% with a high miss-hit ratio, but there is no clear cut answer to which is more impressive.
Thinking about tournaments specifically doesn't really make sense to me. Why would a measure of performance differ on the situation around the play? I, like any reasonable person, am against a scoring system like standard for mania, that gravely punishes players for 1 mess up. The ideal scoring system (other than the unreasonable idea I mentioned in my earlier post) is a system that rewards consistency, but less than accuracy.
I'm confused by what you mean of figuring out consistency map by map. Could you please clarify?
While writing this, I came up with a (probably stupid) idea. The reason I'm not a fan of using combo for consistency is because it is possible to mash through hard patterns and keep combo. Also, I don't think that 1 miss should affect score too much. I mentioned that I like the system of using bonus score. Why don't we make the worth of a note (at least in the consistency portion of score) equal (scaled appropiately obviously) to your current health? Obviously, changes to health would need to be done, to punish any judgement less than a 300. However, maybe with a bunch of tuning, this might work. I'm probably just an idiot tho lol
If you convert acc to score out of 1M as it is right now, 960,000 and 990,000 (96% and 99%) will be a very small gap and is also where most decent plays fall to. Transforming that same gap to 650,000 and 990,000 would allow to highlight skill more clearly. Yes anyone who gets less than an S gets wrecked, but then again you shouldn't be surprised at such results when you play maps out of your skill range.
Maybe the scoring shouldn't be to that extend, but it doesn't seem to be a bad direction. Maybe then less people would complain about smashing maps on an A.
Would time to get used to it though.
hahaha good one
One of the reasons why SS makes no sense is this
source
And if it's not based on 1 000 000 (say it's based on 990 000 or something similar), keep in mind that accuracy now decreases with 300 compared to 300g, just as you get less score with 300 as opposed to 300g. Accuracy affects score, so minuscule mistakes would be a lot more punishing than before.
The only way grades based on score would work is if score is 100% based on accuracy (like DDR), and even then the grades would be based on accuracy by extension.
But again, you lose accuracy now with 300, so the accuracy SS requirement would have to be adjusted.
Ah, I see. Yeah, that works.
However, everything you guys are talking about is unrelated to ScoreV2. I'd appreciate someone giving their thoughts on my ideas (or any other ideas) on the more relevant aspects of ScoreV2.
show more
He means to have options on which scoring method to use. The combo mod in this sense would use the combo based scoring.Full Tablet wrote:
What do you mean by combo mod? What would it do?
In that case, wouldn't it better if both scoring methods were calculated simultaneously for each play, and both values are recorded in the play? In leaderboards, people would have an option to sort by combo scoring or accuracy score.abraker wrote:
He means to have options on which scoring method to use. The combo mod in this sense would use the combo based scoring.Full Tablet wrote:
What do you mean by combo mod? What would it do?
Accuracy score should be the main value used for the rest of the performance and ranking system (as long there is only one ranking based on the one-dimensional pp value of each player), since the count of the judgments is a more reliable statistic to base inferences about the skill of a player, compared to the length of string of non-misses (mixing both by adding two different formulas together doesn't make it better than a pure accuracy-based formula either, the quality of the formula used for overall score increases the lower the weight of the combo portion of it is).
That said, basing the accuracy score on the current Accuracy Percentage formula is not good either. Accuracy Percentage underweights the importance of Rainbows over regular 300s, and overweights the importance of 200s over 100s/50s/Misses.
"Skill" isn't all about accuracy. Although most people agree it should be the largest factor, players have a variety of other skills which some focus more than others and that should deserve some acknowledgement in their score. In this case, it would be for players with the speed/finger dexterity to hit those few extra notes in the hardest part of a map to keep their full combo compared to accuracy players who will skim through that section and perfect everything else on the map.Full Tablet wrote:
Accuracy score should be the main value used for the rest of the performance and ranking system (as long there is only one ranking based on the one-dimensional pp value of each player), since the count of the judgments is a more reliable statistic to base inferences about the skill of a player, compared to the length of string of non-misses (mixing both by adding two different formulas together doesn't make it better than a pure accuracy-based formula either, the quality of the formula used for overall score increases the lower the weight of the combo portion of it is).
The thing is, combo is not a good way to measure the aspect of skill you mention either.Squishykorean wrote:
"Skill" isn't all about accuracy. Although most people agree it should be the largest factor, players have a variety of other skills which some focus more than others and that should deserve some acknowledgement in their score. In this case, it would be for players with the speed/finger dexterity to hit those few extra notes in the hardest part of a map to keep their full combo compared to accuracy players who will skim through that section and perfect everything else on the map.
For measuring the ability of being able to hit hard notes without missing, miss count is a better statistic than a score based on combo.
If you want to isolate speed/dexterity skill from overall accuracy skill, ideally, you should be able to calculate 2 different scores for each aspect of skill, and have two different leaderboards and rankings for the same plays.
So yeah, accuracy is the main value in both score v1 and v2. Combo is important as your score drops if you miss, whats the point of having a "combo mod" then? I dont really get it.
If you are good at doing combos but your acc is really bad why should you win against a good accuracy with some missees? Into a level where everyone misses then yeah, sure, but adding the combo mod wont change stuff imo.
If you are good at doing combos but your acc is really bad why should you win against a good accuracy with some missees? Into a level where everyone misses then yeah, sure, but adding the combo mod wont change stuff imo.
What you (and I) want is better achieved by increasing the significance of a single miss. Accuracy players will be harshly (but fairly) punished for missing, and speed/dexterity players still stand a chance with their lower accuracy and higher combos. If ScoreV2 were to drop the combo component and go this route, we would have a scoring system that...:Squishykorean wrote:
"Skill" isn't all about accuracy. Although most people agree it should be the largest factor, players have a variety of other skills which some focus more than others and that should deserve some acknowledgement in their score. In this case, it would be for players with the speed/finger dexterity to hit those few extra notes in the hardest part of a map to keep their full combo compared to accuracy players who will skim through that section and perfect everything else on the map.Full Tablet wrote:
...
- still rewards players for keeping their combo.
- treats x consequent misses the same as x isolated misses (ScoreV2 punishes isolated misses more severely)
- cannot produce broken scores where similar performances have unexplainable differences, because relatively more 200s were attained at <400 combo.
- can be significantly simpler to understand and implement.
Kempie wrote:
If ScoreV2 were to drop the combo component and go this route, we would have a scoring system that...:
- rewards players for keeping their combo.
When all you do is remove the combo component, misses aren't sufficiently punished for, i.e. keeping combo (not missing) isn't as big of a deal as it should be. By making misses more punishing, you are "rewarding" (more like not punishing) players that do not miss, and thus keep their combo.Ayaya wrote:
Kempie wrote:
If ScoreV2 were to drop the combo component and go this route, we would have a scoring system that...:
- rewards players for keeping their combo.
It sounds confusing because it's sort off tackling the same problem in the exact opposite way. You're not actually rewarding players for keeping high combos, you're just upping the punishment of misses. Fewer misses generally equal higher combo, with edge cases like FC'ing a song and then missing the last 5 notes being an exception to that rule. Unsurprisingly, these edge cases also produce funny scores in ScoreV1/V2, but not in MIGS scoring for example.
I knew what you meant but you just worded that part weird, also I just wanted to use that jpeg 
Yes I would agree punishing misses more harshly would solve much of the problem. The only thing that might make this slightly unattractive is the fact someone might mess up and cause a chain of misses even though they are hitting the notes correctly. The current combo multiplier doesn't punish as hard when this happens because as long as you recover and don't miss later, you are still given a chance at getting a decent score despite a tiny screw up that the game mechanics happened to snowball on.
Would you reward a player that missed 5 notes spread out throughout the map equally to a player who hit a chord wrong and missed 5 consecutive notes together?
This is purely opinion based but what this seems to be turning into is another stepmania scoring system and with lots of players here coming from that game, it would only be natural to lean towards their scoring system.
Would you reward a player that missed 5 notes spread out throughout the map equally to a player who hit a chord wrong and missed 5 consecutive notes together?
This is purely opinion based but what this seems to be turning into is another stepmania scoring system and with lots of players here coming from that game, it would only be natural to lean towards their scoring system.
So you should cater to the people migrating rather than having them adapt or leave like they should?Squishykorean wrote:
This is purely opinion based but what this seems to be turning into is another stepmania scoring system and with lots of players here coming from that game, it would only be natural to lean towards their scoring system.
Getting a chain of misses in isolation is an extremely rare scenario. In hard sections particularly, it is complemented with 100s and 50s, which is the major proportion of the penalty of a general CB rush/bad judgement rush. It's not misses that are particularly penalising despite the slightly higher penalty per judgement, since they happen less frequently than 50s/100s. A CB rush will almost always punish a player far more than misses in isolation, not necessarily because of the combo multiplier, but because of the accuracy component.Squishykorean wrote:
Yes I would agree punishing misses more harshly would solve much of the problem. The only thing that might make this slightly unattractive is the fact someone might mess up and cause a chain of misses even though they are hitting the notes correctly. The current combo multiplier doesn't punish as hard when this happens because as long as you recover and don't miss later, you are still given a chance at getting a decent score despite a tiny screw up that the game mechanics happened to snowball on.
Would you reward a player that missed 5 notes spread out throughout the map equally to a player who hit a chord wrong and missed 5 consecutive notes together?
This is purely opinion based but what this seems to be turning into is another stepmania scoring system and with lots of players here coming from that game, it would only be natural to lean towards their scoring system.
The main ways you can get a massive amount of misses and only misses is if you're very negligent in an easy section (misreads), minor misreads in hard sections (which are generally penalised less anyway) or if you're hitting extremely conservatively in hard sections. Being negligent in an easy section is usually minor (1-2 misses), it's very very rare to actually early miss a massive chord in the first place anyway. And even then, that's an extreme edge case - and an extremely rare scenario that is rarely replicated in normal gameplay and can be discarded as an anomaly in gameplay.
Combo multiplier has the issue of not being able to discriminate between 5 misses spread out in easy sections and 5 misses in a hard section, definitely, but so do misses. Having a combo multiplier is just increasing the magnitude of that source of error. This is ultimately why people don't think combo multiplier is a good idea - it's an unnecessary metric that adds nothing if the game itself does not promote the idea of "perfection". osu!mania does not promote perfection. Otherwise, the PP system would favour more towards 1mil scores rather than 700-850K scores, SR would look at only the hardest part of the chart (it technically does this already if the hard section is long enough, but it doesn't address super short spikes completely well), and non-300 judgements would be far far more punishing.
Since there's not much left to discuss about ScoreV2, I'll just post this interesting MWC match to remind the devs on the severity of MAX's being underrated:
Other scores left out for brevity.
Other scores left out for brevity.
Maybe the 1xgood was too bad for halogen
It's pretty telling that we know how harsh it is given we've also seen what the difference is with individual 300 judgments -- the fact that I got 164 less 300s but only had a single 200 and lost by 350 points when our scores were that high is very telling: 300s are not weighted enough, or judgments beneath that are weighted too heavily (or a combination of the two)...
Yeah, holy crap, that should not happen. If the ratio was closer I could see guil edging that out, but with that much difference in 300's that's pretty insane.
essentially, the mechanic of score in the end should be an indicator of which spread of judgements took more skill to hit
in the example of halogen vs. guilhermeziat, i think pretty much anyone can glance at those judgement spreads and say one is better than the other.
that's not being shown in the actual score however.
in the example of halogen vs. guilhermeziat, i think pretty much anyone can glance at those judgement spreads and say one is better than the other.
that's not being shown in the actual score however.
today's match between Japan and Brazil (and a lot of other matches throughout this tourney featuring dense LN maps) shows how ridiculously difficult the HP penalty is for LN maps. Please take this into consideration and rebalance HP losses and gains on long notes for the future.
ScoreV2 in retrospect (similar to my previous long post, you can just read the bolded parts if you can't be assed):
First things first. While some of these issues were pointed out before MWC started, there also wasn't that much time to actually go about fixing these changes. That doesn't mean I'm going to repost these issues here however. Also, I am mostly going to be reposting issues discovered, along with a few other of my own comments, so this will largely be a post combining info.
One of the major issues found, especially pertaining to high level play, comes from the fact that the accuracy component did not differentiate between 300g's and 300's. This resulted in the weights of the non-perfect judgements counting for far more than they should have, as the only advantage a 300g had was in the combo portion of the score, which was typically extremely small. In a previous post, Shoegazer suggested how we could let 300g's be weighted as a 305 in the accuracy portion of the score. (Smaller than scorev1 due to the exponential vs. linear nature of this portion of the score). A naive implementation of this, however, would make SS's pretty much non-existent, which I am not sure is good for the overall state of the game (as getting rid of an entire grade seems like a bad idea). When MWC 7k rolls around next year and people start actually caring about this again, it would be a good idea to start by testing out this change, especially as it significantly affects score in the earlier stages of a tournament.
At the time of my previous post, I mentioned how the ending window of LNs should be loosened a bit. As it turns out, there was never any extra leniency for releases in the first place, and for the most part, it now looks pretty fine. Overall, it is still more difficult to get good accuracy on LNs like before, but that is fine.
However, LNs still run into 2 problems. First of all, the HP drain rate (and health mechanics related to LNs) are generally fucked. This is due to a couple of reasons:
To be perfectly honest, this barely mattered at all during the tournament, as for the most part, the player/team with the better accuracy won. Other than the fact that the notes at the beginning of the song are weighted less than notes after the 400th notes, which can most certainly be fixed in the future, there is not really enough enough experimental evidence, especially with scores that aren't this high, in order to see what effect this really has. This probably has to be put off for a more large scale test in the future, especially considering outliers that have good acc/bad combo, and those that have bad acc/good combo.
First things first. While some of these issues were pointed out before MWC started, there also wasn't that much time to actually go about fixing these changes. That doesn't mean I'm going to repost these issues here however. Also, I am mostly going to be reposting issues discovered, along with a few other of my own comments, so this will largely be a post combining info.
300g's and 300's
One of the major issues found, especially pertaining to high level play, comes from the fact that the accuracy component did not differentiate between 300g's and 300's. This resulted in the weights of the non-perfect judgements counting for far more than they should have, as the only advantage a 300g had was in the combo portion of the score, which was typically extremely small. In a previous post, Shoegazer suggested how we could let 300g's be weighted as a 305 in the accuracy portion of the score. (Smaller than scorev1 due to the exponential vs. linear nature of this portion of the score). A naive implementation of this, however, would make SS's pretty much non-existent, which I am not sure is good for the overall state of the game (as getting rid of an entire grade seems like a bad idea). When MWC 7k rolls around next year and people start actually caring about this again, it would be a good idea to start by testing out this change, especially as it significantly affects score in the earlier stages of a tournament.
LNs
At the time of my previous post, I mentioned how the ending window of LNs should be loosened a bit. As it turns out, there was never any extra leniency for releases in the first place, and for the most part, it now looks pretty fine. Overall, it is still more difficult to get good accuracy on LNs like before, but that is fine.
However, LNs still run into 2 problems. First of all, the HP drain rate (and health mechanics related to LNs) are generally fucked. This is due to a couple of reasons:
- In Scorev1, simply holding an LN wouuld give you a small increase in HP every combo tick. This originally was not present in v2, but this was apparently fixed by smoogi before the tournament. I suspect then, that the main reason for the HP drain being fucked comes from the next point.
- While each normal note can only be "missed" once, you can actually miss a LN up to 3 times. The points where you can miss are namely: the LN start, the LN end, and releasing a held LN (resulting in a HoldBreak or whatever, can't be assed to search it up). In addition, if you don't have the LN start, or break the hold, you automatically reduce the highest judgement for the LN end to 50, hampering HP gain even more. Compare this to Scorev1, where you could only miss twice (one of the contributing reasons to why LN maps are harder to maintain HP in as well).
The Combo Portion
To be perfectly honest, this barely mattered at all during the tournament, as for the most part, the player/team with the better accuracy won. Other than the fact that the notes at the beginning of the song are weighted less than notes after the 400th notes, which can most certainly be fixed in the future, there is not really enough enough experimental evidence, especially with scores that aren't this high, in order to see what effect this really has. This probably has to be put off for a more large scale test in the future, especially considering outliers that have good acc/bad combo, and those that have bad acc/good combo.
Not sure if I understand this correctly, but if I do,
300g has been hit in two ways in scorev2:
1. Not playing a role anymore in multipliers.
The main difference between 300g and 300 other than HitValue was the HitBonus allowing more accurate players to more quickly make up for the score deficit after a mistake. The removal of HitPunishment and HitBonus means there's no difference in the following notes. Your combo multiplier increases the same way whether you get a 200, 300 or 300g. Literally there's a 1/16 raw score difference on a single note between the two judgments, which is in turn affected by:
(as mentioned multiple times)
2. Being confined in the combo portion of scoring.
80% of the score AND the multiplier (the main point!) of the remaining 20% portion have nothing to do with your 300g ratio. This results in a pathetic actual difference between the two judgments, and players with no actual sense of rhythm get scores like this: (forgot mp link, but the others had about 3:1 300g ratio give or take)
hue
Personally I agree with the 300g -> 305 idea, and to preserve the practicality of grades may I dare suggest the ridiculous idea of having TWO accuracy calculated: a displayed accuracy and an actual accuracy. The displayed accuracy does not differentiate between 300g's and 300's while the actual accuracy used in the scoring does. This is kind of like scorev1 though.
300g has been hit in two ways in scorev2:
1. Not playing a role anymore in multipliers.
The main difference between 300g and 300 other than HitValue was the HitBonus allowing more accurate players to more quickly make up for the score deficit after a mistake. The removal of HitPunishment and HitBonus means there's no difference in the following notes. Your combo multiplier increases the same way whether you get a 200, 300 or 300g. Literally there's a 1/16 raw score difference on a single note between the two judgments, which is in turn affected by:
(as mentioned multiple times)
2. Being confined in the combo portion of scoring.
80% of the score AND the multiplier (the main point!) of the remaining 20% portion have nothing to do with your 300g ratio. This results in a pathetic actual difference between the two judgments, and players with no actual sense of rhythm get scores like this: (forgot mp link, but the others had about 3:1 300g ratio give or take)
hue
Personally I agree with the 300g -> 305 idea, and to preserve the practicality of grades may I dare suggest the ridiculous idea of having TWO accuracy calculated: a displayed accuracy and an actual accuracy. The displayed accuracy does not differentiate between 300g's and 300's while the actual accuracy used in the scoring does. This is kind of like scorev1 though.
Where can I see the current characteristics of scoreV2 ? The OP is outdated and I honestly don't want to read through the 25 pages of this post
Also why does FlashLight give a multiplier but FadeIn doesn't when there are some people who perform better with FL than NoMod but not a single one in the world who performs better with FI than NoMod? (I can tell by the "global rankings with active mods" that I am the only one in the world who uses FI for topscores, and even I only do it because it's a fun challenge, it's actually a handicap to my performance)
Also why does FlashLight give a multiplier but FadeIn doesn't when there are some people who perform better with FL than NoMod but not a single one in the world who performs better with FI than NoMod? (I can tell by the "global rankings with active mods" that I am the only one in the world who uses FI for topscores, and even I only do it because it's a fun challenge, it's actually a handicap to my performance)
I think you are like 3 months late. Pretty sure you can use the search function here.LastExceed wrote:
Where can I see the current characteristics of scoreV2 ? The OP is outdated and I honestly don't want to read through the 25 pages of this post
Also why does FlashLight give a multiplier but FadeIn doesn't when there are some people who perform better with FL than NoMod but not a single one in the world who performs better with FI than NoMod? (I can tell by the "global rankings with active mods" that I am the only one in the world who uses FI for topscores, and even I only do it because it's a fun challenge, it's actually a handicap to my performance)
why 3 months late? also what am I supposed to search for?juankristal wrote:
I think you are like 3 months late. Pretty sure you can use the search function here.LastExceed wrote:
Where can I see the current characteristics of scoreV2 ? The OP is outdated and I honestly don't want to read through the 25 pages of this post
Also why does FlashLight give a multiplier but FadeIn doesn't when there are some people who perform better with FL than NoMod but not a single one in the world who performs better with FI than NoMod? (I can tell by the "global rankings with active mods" that I am the only one in the world who uses FI for topscores, and even I only do it because it's a fun challenge, it's actually a handicap to my performance)
juankristal wrote:
I think you are like 3 months late. Pretty sure you can use the search function here.LastExceed wrote:
Where can I see the current characteristics of scoreV2 ? The OP is outdated and I honestly don't want to read through the 25 pages of this post
Also why does FlashLight give a multiplier but FadeIn doesn't when there are some people who perform better with FL than NoMod but not a single one in the world who performs better with FI than NoMod? (I can tell by the "global rankings with active mods" that I am the only one in the world who uses FI for topscores, and even I only do it because it's a fun challenge, it's actually a handicap to my performance)
This is actually not late at all, we should be slowly starting to get back into discussions about v2 because 7K MWC is right after OWC which is about to start.
Just seems like no one cares anymore...
Sure thing, it is still a long way to go but same thing we said last time.-Kamikaze- wrote:
This is actually not late at all, we should be slowly starting to get back into discussions about v2 because 7K MWC is right after OWC which is about to start.
The point here is that in order to advance is not that we really need much more stuff to talk about. We saw results in the MWC4K and what we can do is just post solutions to the problem (even tho this has been done already before and we all know what happened). Hopefully those points will be used for this 7K World Cup.
still need an answer to my question though
why does FlashLight give a multiplier but FadeIn doesn't when there are some people who perform better with FL than NoMod but not a single one in the world who performs better with FI than NoMod? (I can tell by the "global rankings with active mods" that I am the only one in the world who uses FI for topscores, and even I only do it because it's a fun challenge, it's actually a handicap to my performance)
you are automatically assuming that noone can do FI just as good or better than nomod, so that's already a dumb point. It's all a matter of prefference, for example Tidek can do even better on FI than on nomod on some maps (he A'd blastix riotz with FI for example tho not pb)
I can hardly believe that it increases his performance and he just doesn't want to use it.-Kamikaze- wrote:
you are automatically assuming that noone can do FI just as good or better than nomod, so that's already a dumb point. It's all a matter of prefference, for example Tidek can do even better on FI than on nomod on some maps (he A'd blastix riotz with FI for example tho not pb)
It's probably only because he can't reach a high combo on that map (as you said it's "just" an A) so the shadow didn't go very low
I'm gonna ask him that personally to clear this up. Any other potential FI players you know of? I am always searching
But even if there are a few players who can play better with FI and they just don't want to, the amount is still way smaller than FL players so the point persists.
that would not be the case fyi if FI worked as it actually should work. at the moment the cover goes way too low, making it reaaaaaaaaally hard to read on default hitposition and that's pretty much the only reason why a lot of people tend to make skinned lanecovers instead. a lot of people in BMS, IIDX and even here use a lanecover that covers the screen in the same way as FI, but without the effect of it "growing" and it does help them a lot. some examples:
yeah I am aware of people using lane covers, I always thought that the difficulty of FI lays in its crazy scaling and I wish that I could get some sort of reward for handicapping myself with it one day, especially now that combo is getting some value in mania...
The growing effect is exactly what makes FI a whole lot harder. Getting good with FI means:-Kamikaze- wrote:
.... a lot of people in BMS, IIDX and even here use a lanecover that covers the screen in the same way as FI, but without the effect of it "growing" and it does help them a lot....
- You have to get used to the ridiculously shallow visibility maxed out FI provides.
- You have to deal with misses fucking up FI's shadow.
I know, and this is kinda what I mean, FI's design is flawed whether it's "growing" too far, from too high starting point or "growing" at all.
I have heard before that with v2 optimizations for next MWC there can be changes in mods, so I would suggest making both hidden and fadein either grow but from much higher point and not as far up/down or just be stable at like 2/3 up/down of the way from your hitposition to the edge of the screen and (this has to be done to make FI even semi viable) fixate cover of FI/HD to hitposition.
This is the main reason why FI is so hard to most, you can deal with the growing in various ways (like even putting a shirt on monitor) but it grows too far down to be able to handle dense patterns since you have to drastically lower your speedmod.
Talking about mods and score multipliers - after watching the last MWC I do think that both HR and FL/FI/HD should actually have the same multiplier and have the multiplier be 1,06x since up until finals (and even at that stage there were maps where this applied) using HR on freemods was nearly always a net positive. It was actually quite hard to get a lower score using HR than you would using nomod, because the score buffer on HR was more than enough to cover for lower acc. HR should be a risky mod for those who are REALLY confident they can do well on a map. That multiplier also made visual mods (FL there, but I'm talking about all for the sake of the future) unviable unless you were doing HR already, due to the lower multiplier. There should be multiple tactical avenues you can take on that and FL vs HR for example should be a good one.
I am aware that there are players that can do better with FL/HD/whatever than nomod, but that kinda eliminates them from nomod bracket, so it's another wrinkle on the player picking strategy for the capains which is nice.
Also there is a biiiig problem as explained before with LN drain being too high (both start and end drain the same amount of hp as normal notes which is a killer, imo it should be about 70% for the start and 30% for the release), MAX:300 ratio being underrated as fuck:
I have heard before that with v2 optimizations for next MWC there can be changes in mods, so I would suggest making both hidden and fadein either grow but from much higher point and not as far up/down or just be stable at like 2/3 up/down of the way from your hitposition to the edge of the screen and (this has to be done to make FI even semi viable) fixate cover of FI/HD to hitposition.
This is the main reason why FI is so hard to most, you can deal with the growing in various ways (like even putting a shirt on monitor) but it grows too far down to be able to handle dense patterns since you have to drastically lower your speedmod.
Talking about mods and score multipliers - after watching the last MWC I do think that both HR and FL/FI/HD should actually have the same multiplier and have the multiplier be 1,06x since up until finals (and even at that stage there were maps where this applied) using HR on freemods was nearly always a net positive. It was actually quite hard to get a lower score using HR than you would using nomod, because the score buffer on HR was more than enough to cover for lower acc. HR should be a risky mod for those who are REALLY confident they can do well on a map. That multiplier also made visual mods (FL there, but I'm talking about all for the sake of the future) unviable unless you were doing HR already, due to the lower multiplier. There should be multiple tactical avenues you can take on that and FL vs HR for example should be a good one.
I am aware that there are players that can do better with FL/HD/whatever than nomod, but that kinda eliminates them from nomod bracket, so it's another wrinkle on the player picking strategy for the capains which is nice.
Also there is a biiiig problem as explained before with LN drain being too high (both start and end drain the same amount of hp as normal notes which is a killer, imo it should be about 70% for the start and 30% for the release), MAX:300 ratio being underrated as fuck:
Ciel's post explains some of the issues as well: link for convenience sake.Kempie wrote:
Since there's not much left to discuss about ScoreV2, I'll just post this interesting MWC match to remind the devs on the severity of MAX's being underrated:
Other scores left out for brevity.
I have heard before that with v2 optimizations for next MWC there can be changes in modsthis would be some good news
I would suggest making both hidden and fadein either grow but from much higher point and not as far up/down or just be stable at like 2/3 up/down of the way from your hitposition to the edge of the screenmaking them smaller would result in even more people using them out of preference, and a fixed shadow would be boring (i find the scaling very fun so we should keep that. Yiu're right, somethng should change, but not like this.
fixate cover of FI/HD to hitpositionyeah this makes sense
you have to drastically lower your speedmod.you're overseeing something important here: yes you do have to slow down, but only as much as people like me (who play with low speed by default) have to speed up in order to play hidden. To me HD is as hard as FI is to you. This is also why i think the maximum scale doesn't necessarily have to be changed that much, if at all.
Talking about mods and score multipliers (...)All i can say here is that HR is too high, because even I (who has a horrible acc) get better scores with it. Balancing HR and visual mods would only be useful for tournaments, and I am not sure if that's really worth it.
I have no feeling for score or hp values because i have too few experience with v2 so i can't give an opinion on that.
Kamikaze is a nice guy. Although our opinions almost ALWAYS differ, its nice to have him in debates like these because he brings the discussion forwards alot by always staying on topic and serving good arguments for everything. A rare ability I really appreciate.
LastExceed wrote:
I would suggest making both hidden and fadein either grow but from much higher point and not as far up/down or just be stable at like 2/3 up/down of the way from your hitposition to the edge of the screenmaking them smaller would result in even more people using them out of preference, and a fixed shadow would be boring (i find the scaling very fun so we should keep that. Yiu're right, somethng should change, but not like this.
Bolded the sentence on purpose - the fact that you find scaling fun does not mean that it should be the way it's done. It's just personal bias. Also the way I see it - the initial cover should be larger for both FI/HD so it's not that much of a mindfuckyou have to drastically lower your speedmod.you're overseeing something important here: yes you do have to slow down, but only as much as people like me (who play with low speed by default) have to speed up in order to play hidden. To me HD is as hard as FI is to you. This is also why i think the maximum scale doesn't necessarily have to be changed that much, if at all.
That is actually not true. I play at a relatively average speedmod (25-26) and I can read hidden fine with that speed (or 1 higher), while for FI on default hitposition I have to use speed 9. Tidek as another example usually plays on speed around 22-23 (iirc) and he also took down his to 11 with lower hitposition while he learned how to do hidden before it was removed from mod pool for the last mwc and I'm pretty sure that he didn't up the scroll speed too much if at all. You also missed the point that you have to drastically decrease it and that the field of vision is too low with default hitposition, and I believe that if the cover area is fixated not to the edge of the screen but to the hitposition the field of vision will already be a decent bit bigger.Talking about mods and score multipliers (...)All i can say here is that HR is too high, because even I (who has a horrible acc) get better scores with it. Balancing HR and visual mods would only be useful for tournaments, and I am not sure if that's really worth it.
I have no feeling for score or hp values because i have too few experience with v2 so i can't give an opinion on that.
Even if it's only for tournament purposes it's still hella worth it, you would like to see a fair tournament with interesting scoring and mod mechanics more than one with broken ones would you?
Kamikaze is a nice guy. Although our opinions almost ALWAYS differ, its nice to have him in debates like these because he brings the discussion forwards alot by always staying on topic and serving good arguments for everything. A rare ability I really appreciate.
oh, thanks haha I appreciate that
The previous formulas I proposed (based on fitting the timings of the play to a normal distribution) become, simpler, more accurate, and faster to calculate if one uses the exact timing of each hit instead of the judgment counts.
How would the scoring system work:
1) Take the exact error of each note that was hit. For LN releases, divide it's error by x1.5 (to account for the fact that it's harder to time releases than hits), the multiplier could be adjusted to other value. Do not consider hits/releases that were hit in their "Miss" timing window.
Take the sum of the squares of those errors (that value will be referred as "s"), and the count of the hits and releases that weren't misses (referred as "k").
2) Count the amount of misses notes and releases (referred as "m").
3) With that information, calculate the Normal Distribution with zero mean that fits the data the best, obtaining the standard error Sigma (details of the calculation below).
4) Use a scaling function that maps that standard error to a score. A good choice for this function is, for Sigma measured in ms:
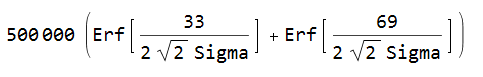
Erf is the Error Function. In the case Sigma is zero (which is only possible with a perfect play, which should be almost certainly impossible), then the score is 1 million.
For EZ/HT, for balance, it would be best if they don't change the timing window for 50s nor the timing window for Misses. That way, they can't have an effect on score, they become merely cosmetic (changing the distribution of the judgments during the play). DT/HT shouldn't change the timing window of 50s and Misses either (besides scaling to make internal clocks match real time, like it is done currently). To make scores with different ODs in the same map be directly comparable, those timing windows shouldn't change either (this way, OD becomes merely cosmetic as well while playing).
How would the scoring system work:
1) Take the exact error of each note that was hit. For LN releases, divide it's error by x1.5 (to account for the fact that it's harder to time releases than hits), the multiplier could be adjusted to other value. Do not consider hits/releases that were hit in their "Miss" timing window.
Take the sum of the squares of those errors (that value will be referred as "s"), and the count of the hits and releases that weren't misses (referred as "k").
2) Count the amount of misses notes and releases (referred as "m").
3) With that information, calculate the Normal Distribution with zero mean that fits the data the best, obtaining the standard error Sigma (details of the calculation below).
4) Use a scaling function that maps that standard error to a score. A good choice for this function is, for Sigma measured in ms:
Erf is the Error Function. In the case Sigma is zero (which is only possible with a perfect play, which should be almost certainly impossible), then the score is 1 million.
For EZ/HT, for balance, it would be best if they don't change the timing window for 50s nor the timing window for Misses. That way, they can't have an effect on score, they become merely cosmetic (changing the distribution of the judgments during the play). DT/HT shouldn't change the timing window of 50s and Misses either (besides scaling to make internal clocks match real time, like it is done currently). To make scores with different ODs in the same map be directly comparable, those timing windows shouldn't change either (this way, OD becomes merely cosmetic as well while playing).
Calculating the Standard Error "Sigma"
The variables are:
s = Sum of the squares of the timing errors of hits/releases that weren't a Miss. (Releases with errors scaled by a constant)
k = Count of hits/releases that weren't a Miss.
m = Count of Misses.
T = Upper limit of the timing window for a 50, in ms.
Case with no Misses
Sigma is simply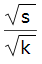
Case with Misses
Sigma is the positive number that solves the equation:
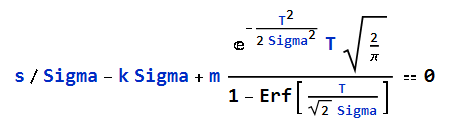
The equation doesn't have a simple closed form solution, but it can be easily solved numerically with Newton's Method (since the function to find a root for is convex and monotonic).
A first approximation of Sigma (that always is smaller than the real solution) is:
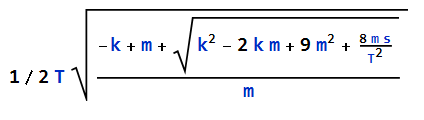
With BS = T/Sigma.
Function to find the root for:
It's derivative: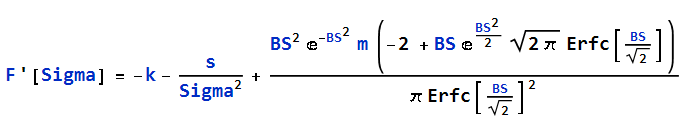
Note: Because of numerical errors while using double floating-point numbers to calculate the functions, for high values of BS, it's more accurate to use a series expansion near Sigma=0, instead of attempting to calculate their values with the exact formulas.
If BS > 7, then: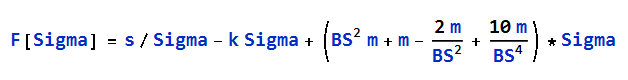
If BS >20, then: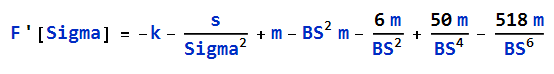
The, starting with the initial approximation for sigma, iterate with Newton's Method until F[Sigma] is small:
Sigma[n+1] = Sigma[n] - F[Sigma[n]] / F'[Sigma[n]]
Testing this algorithm, it takes about 0.8ms in average to find an accurate value for Sigma (with an absolute error of 10^(-7)).
s = Sum of the squares of the timing errors of hits/releases that weren't a Miss. (Releases with errors scaled by a constant)
k = Count of hits/releases that weren't a Miss.
m = Count of Misses.
T = Upper limit of the timing window for a 50, in ms.
Case with no Misses
Sigma is simply
Case with Misses
Sigma is the positive number that solves the equation:
The equation doesn't have a simple closed form solution, but it can be easily solved numerically with Newton's Method (since the function to find a root for is convex and monotonic).
A first approximation of Sigma (that always is smaller than the real solution) is:
With BS = T/Sigma.
Function to find the root for:
It's derivative:
Note: Because of numerical errors while using double floating-point numbers to calculate the functions, for high values of BS, it's more accurate to use a series expansion near Sigma=0, instead of attempting to calculate their values with the exact formulas.
If BS > 7, then:
If BS >20, then:
The, starting with the initial approximation for sigma, iterate with Newton's Method until F[Sigma] is small:
Sigma[n+1] = Sigma[n] - F[Sigma[n]] / F'[Sigma[n]]
Testing this algorithm, it takes about 0.8ms in average to find an accurate value for Sigma (with an absolute error of 10^(-7)).
That looks pretty impressive, I'll have to read into it later though (currently at work).
As good as it might be, I do think you're wasting your time. Quoting from Smoogipoo's askfm:
So basically; calm down and suck up to scorevcombo
As good as it might be, I do think you're wasting your time. Quoting from Smoogipoo's askfm:
Answered ~4 months ago.Anonymous questioner wrote:
Will you keep trying with different versions of scorev2 for mania? The current iteration is more a compromise between what players want, and what the game developers think it should be, instead of what players really want with the score system.
http://ask.fm/smoogipooo/answers/138940251287smoogi~ wrote:
Yeah. I've just been busy the past week with exams and will continue to be busy in the coming week with the same...
But let me address something. Combo _will_ remain regardless of iteration. It is not going anywhere. So if "what players really want" is for scoring to be an accuracy-only model, forget it.
Likewise, if players want us to copy another game's scoring system, forget it. If players want us to make a massively complex scoring system that takes into account difficult in sections of the maps and/or requires careful analysis of the timing distributions of hits, forget it.
But why, why will combo remain? You HAVE to realize that ScoreV2 is going to be used for MWC, and there are other aspects to consider in such an environment to make gameplay more exciting and to really show off the best-of-the-best. I've explained this before on reddit/the forums.
The scoring system must be easily able to be changed/recomputed and must be easy to use for _all_ other modes with minimal to no modification. Yes, this is "what the developers want", because we want to be able to re-balance the meta easily in the future.
So basically; calm down and suck up to scorevcombo
I'd like to know as well.ReTLoM wrote:
Any news cause 7k MWC isnt far anymore
So, gonna start this train now: adjust LN life weighting so that heads/tails are 0.5x of normal, as a miss of a head almost certainly means you're missing a tail and you shouldn't be penalized twice as harshly for missing a LN than you would a normal tap, haha
this incorrect life weighting caused a *lot* of fails in 4K MWC because LN's were mathematically twice as harsh in penalty.
this incorrect life weighting caused a *lot* of fails in 4K MWC because LN's were mathematically twice as harsh in penalty.
Reposting this as well; considering that rainbow accuracy is a major component in assessing skill, I think embedding higher emphasis in rainbow accuracy will make the scorev2 system more accurate when it comes to assessing skill.Shoegazer wrote:
Rainbow AccuracyI initially wanted to increase the rainbow judgement weightage without embedding rainbows into accuracy, but no matter how much I changed it, the difference is very minor (~600-1,200 points) and a 200 will almost always be too powerful compared to a rainbow 300. So I scrapped that idea and thought that embedding rainbows into accuracy with a reasonable weightage and maybe making the curve more lenient would be the best idea.Shoegazer wrote:
320s are very much underweighted because the only component of the scoring system that takes into account 320 accuracy is the combo component, which only has a 20% prominence. Add on to the fact that the difference between a 300 and 320 is so small and that the absolute difference between juan and Hudo's 320 count isn't that significant, it would make sense that 320s are really underweighted at the moment.
You could mitigate this by including 300gs into accuracy, but from what I've experimented it might create too much emphasis on MAX accuracy with charts that players have issues getting 96%+ on (and as a result would not be an accurate assessment of skill).Alternatively, you can avoid including MAXes in the accuracy component and just increase the importance of MAXes to like 360 to increase the emphasis of it by a noticeable but not overpowering amount in the combo component, but that requires a bit more experimentation.
I've been experimenting with weightages and discussing with people about how much a 200 should be worth compared to a 300. I initially thought that 310 would be fine (and a 200 would be worth 11 300s), but when it came to matches like this, if accuracy was the only factor, Argentina would win by 21,000 points. I do think that Argentina should win and it's a step in the right direction, but 21,000 seems extremely overwhelming since it undermines the fact that Poland had overall, noticeably less 200s. I tried it with harder charts too and they seem to favour rainbow accuracy a little too much for my liking - especially since when it comes to harder charts (where players struggle with), good rainbow accuracy is usually caused by variance rather than a higher skill level. 200s and worse judgements should determine performance for that.
I wanted to use 307 afterwards, but it still gave a bit too much emphasis for my liking, about 12,500 points for that Argentina/Poland match. I went down to 305, and the difference is about 6,800. I think that's ultimately the most reasonable assessment, and others I've talked to seem to agree with the prenotion that a 200 is about 21 normal 300s. Ignoring the bad judgements (since those values are pretty much set in stone at this point), this is probably (part of) the ideal solution. This does mean that only full rainbow scores are SSs, but I don't see that as a problem as frames of reference can be shifted.
Getting rid of the difference between a rainbow and a normal 300 in the combo scoring component is probably ideal too, since that should be in the accuracy component, not the combo component. If rainbows are included into accuracy, the combo component does not need a rainbow component.
I also wanted to soften the exponential curve a tiny bit when it comes to including rainbows, mainly because at a certain point extremely good accuracy is more caused by variance rather than a very high skill level - unless the performance is consistently done, which is not measurable with just one match and one attempt. The exponential I had in mind was Accuracy^(2 + 2 * Accuracy), but it's essentially Accuracy^4 - so 1 power down.
tl;dr: Embed rainbows into accuracy with a weightage of 305 instead of 320, change the accuracy curve to Accuracy^(2 + Accuracy * 2), remove the differentiation between rainbows and normal 300s in the combo component (both of them should have a HitValue of 30).
I don't think making SS max scores only is a good idea, with how hard it is. the accuracy needed for hitting only 300g is at a completely other level than any other mode. I gueninely hope it's not planned for osu!lazer and is just a tournament thing
Topic Starter
Who cares, this is only for tournament/MWC for now. Ideally come osu!next if this is the best path forward, osu!mania should have an SSS ranking.
That would be amazing actually.smoogipooo wrote:
Who cares, this is only for tournament/MWC for now. Ideally come osu!next if this is the best path forward, osu!mania should have an SSS ranking.
if there's such thing as an SSS or SS+, I can already see the achievement's description "Beyond perfection."smoogipooo wrote:
Who cares, this is only for tournament/MWC for now. Ideally come osu!next if this is the best path forward, osu!mania should have an SSS ranking.
Well, I'm gonna be screwed as soon as this launches.
;-; [*] R.I.P
Wouldn't it be something if they got rid of FL and kept HD and FI (Which should be called sudden) but put FI where FL was such that if you had both enabled it would function as FLRedon wrote:
FI is a stupid idea and needs to be removed completely
FL and HD need to simply not influence score or pp at all because they are purely a question of player preference.
HD should be changed into a customizable lane cover that can either be static or grow in either direction, replacing both HD and FI.
There, I solved it all for you.
Now that a non-shiny 300 doesn't give 100% acc anymore, does that mean an SS in scoreV2 is as rare as a million in scoreV1 ? that imagination really doesn't feel right...
The big differences are the the fact that FL doesn't scale and that it covers the entire screen while the FI/HD shadow only covers the stage.
no srsly FI can be really fun, there's no reason to remove it.
FI + HD =/= FLTachyon wrote:
Wouldn't it be something if they got rid of FL and kept HD and FI (Which should be called sudden) but put FI where FL was such that if you had both on it would function as FL
The big differences are the the fact that FL doesn't scale and that it covers the entire screen while the FI/HD shadow only covers the stage.
being the FI guy I feel like its my duty to say this: "DUN DELET FAD-EN!1!!11one!"Redon wrote:
FI is a stupid idea and needs to be removed completely
FL and HD need to simply not influence score or pp at all because they are purely a question of player preference.
HD should be changed into a customizable lane cover that can either be static or grow in either direction, replacing both HD and FI.
There, I solved it all for you.
no srsly FI can be really fun, there's no reason to remove it.
Found a small issue with SV2. When you initially play a file, you are given a different accuracy percent than you get after reloading osu.
Perhaps osu calculates sv2 mod scores with sv1 after a reload of osu.
This was the screenshot I took right after playing a file.
This was a screenshot of the same play, same score, but the accuracy is markedly higher.
Perhaps osu calculates sv2 mod scores with sv1 after a reload of osu.
This was the screenshot I took right after playing a file.
This was a screenshot of the same play, same score, but the accuracy is markedly higher.
LastExceed wrote:
Now that a non-shiny 300 doesn't give 100% acc anymore, does that mean an SS in scoreV2 is as rare as a million in scoreV1 ? that imagination really doesn't feel right...
The only reason it doesn't feel right is because you are used to the current system. Having a judgement below the highest one negatively impact accuracy makes way more sense if you get out of the old frame of mind.
edit: confusing terminology
Cuber wrote:
The only reason it doesn't feel right is because you are used to the current system. Having a judgement below the highest one negatively impact accuracy makes way more sense if you get out of the old frame of mind.
edit: confusing terminology
I don't think thats the issue here. Im completely fine with all scores dropping little and S ranks becoming harder when scoreV2 goes live because i know that relatively it stays the same (I just need to get used to the new standards) but making a whole rank a once-in-a-lifetime experience is like turning it into an achievement. Imagine how the user profiles would look like, most people would have 0 SS ranks. Further more: mania is the mode with the easiest S ranks in osu!. With scoreV2 as it is it would get the hardest SS ranks which is quite a contrast.
It's a good thing that non-shiny 300s do not give 100% accuracy. When they give 100%, the acc% value becomes an imprecise measure of accuracy at high accuracy levels (for example, there is a big difference between a SS with 1:3 300:300g ratio, and a SS with 1:10 300:300g ratio).
A better solution for the problem of SSs being too rare, is changing the requirements for a SS.
A better solution for the problem of SSs being too rare, is changing the requirements for a SS.
Thats true. Time to bring the SSS rank hereFull Tablet wrote:
It's a good thing that non-shiny 300s do not give 100% accuracy. When they give 100%, the acc% value becomes an imprecise measure of accuracy at high accuracy levels (for example, there is a big difference between a SS with 1:3 300:300g ratio, and a SS with 1:10 300:300g ratio).
A better solution for the problem of SSs being too rare, is changing the requirements for a SS.
I don't think you really understood either post very well, what I meant is that if you enabled both mods it should function the way FL does at the moment, and Redon specified thatLastExceed wrote:
FI + HD =/= FL
The big differences are the the fact that FL doesn't scale and that it covers the entire screen while the FI/HD shadow only covers the stage.being the FI guy I feel like its my duty to say this: "DUN DELET FAD-EN!1!!11one!"Redon wrote:
FI is a stupid idea and needs to be removed completely
FL and HD need to simply not influence score or pp at all because they are purely a question of player preference.
HD should be changed into a customizable lane cover that can either be static or grow in either direction, replacing both HD and FI.
There, I solved it all for you.
no srsly FI can be really fun, there's no reason to remove it.
HD should be changed into a customizable lane cover that can either be static or grow in either direction, replacing both HD and FI.
oh ok yeah that makes more sense.Tachyon wrote:
I don't think you really understood either post very well, what I meant is that if you enabled both mods it should function the way FL does at the moment, and Redon specified that
HD should be changed into a customizable lane cover that can either be static or grow in either direction, replacing both HD and FI.lane covers can already be skinned, there wouldn't be a need for a mod at all anymore. Also there are some people (like me) who actually like the fact that the shadow scales with combo, it just needs to be fixed so that the shadow size adapts to scrollspeed (or bpm if you play bpm scale)
Wowow guys we're getting off-topic here, how did we get from "improve scorev2" to "SSS" and "remove FI" ?
How about we don't remove FI, why remove features when we already got so few. I'd rather see new mods instead.
And I think we already agreed that the 3 visual mods shouldn't give score rewards, because it wouldn't make any sense to do so.
Further on, if we are clear about them being only preferential, It would make sense to even enable them for Nomod maps in tournaments, even if it sounds a bit weird.
Now to the idea of an SSS, uhmm no.
This is still osu so the ranks should be the same for all modes.
Now there are two ways to go about this.
- either say that an SS isn't 100% anymore, and you can only have a certain percentage of normal 300s or something like that
- or make normal 300s be 100% again, which is like starting out from the old system again.
But yeah otherwise rip accuracy players, only gonna see SS on 1-2* maps then.
How about we don't remove FI, why remove features when we already got so few. I'd rather see new mods instead.
And I think we already agreed that the 3 visual mods shouldn't give score rewards, because it wouldn't make any sense to do so.
Further on, if we are clear about them being only preferential, It would make sense to even enable them for Nomod maps in tournaments, even if it sounds a bit weird.
Now to the idea of an SSS, uhmm no.
This is still osu so the ranks should be the same for all modes.
changing the requirements for an SSseems to be the best solution here.
Now there are two ways to go about this.
- either say that an SS isn't 100% anymore, and you can only have a certain percentage of normal 300s or something like that
- or make normal 300s be 100% again, which is like starting out from the old system again.
But yeah otherwise rip accuracy players, only gonna see SS on 1-2* maps then.
SS requirement should be "only 300 and 300r" just like it is right now
Why not just including a SSS for people who gets a perfect score a much better reward and the fact that the 300 now drop the accuracy is a bit of a problem cause it'll be a lot harder for players to have a decent accuracy
This. In DDR, you get an AAA (SS) for getting a score of 990,000 (or 99% accuracy). You get this score if you get all perfects (non-shiny 300s) but no marvelous (rainbow 300s). I know the system here isn't exactly like the one in DDR, as getting all non-shiny 300s will net you a 98.36%, but we should lower the SS requirement to something similar. As previously stated, maybe add an SSS for a perfect 100%.Full Tablet wrote:
A better solution for the problem of SSs being too rare, is changing the requirements for a SS.
As i already said, it's highly unlikely that there will be an SSS added, since there is no equivalent in the other game modes.
But yes the SS criterias should be lowered, it's too difficult to get all max 300s. But what should the ratio required for an SS be ?
How about only 300s but a 1:5 300s to max ratio ? Does that sound rational ?
But yes the SS criterias should be lowered, it's too difficult to get all max 300s. But what should the ratio required for an SS be ?
How about only 300s but a 1:5 300s to max ratio ? Does that sound rational ?
Why are the grades even based on accuracy at all? If score is a measurement of performance in a map, obviously the grading should be based on that and that alone! All grades do in my mind anyways is provide goals that feel more real than reaching an arbitrary number. On this train of thought, PP should also be entirely based on song difficulty and score.
But this thread is about scorev2 lol. Personally, I think that scorev2 taking into account combo is bad (controversial I know). I much prefer the way that scorev1 tries to reward consistency: with a bonus score that fluctuates depending on how you're doing. I'd love to see that incorporated into scorev2. Personally, I think the best possible scoring system is a scoring system that has notes worth less or more, depending on how hard the map is at that point. This is probably unrealistic since this would need a good way to measure difficulty, and star rating has proven itself to not be very good, especially at harder maps. Still could be interesting to try IDK.
But this thread is about scorev2 lol. Personally, I think that scorev2 taking into account combo is bad (controversial I know). I much prefer the way that scorev1 tries to reward consistency: with a bonus score that fluctuates depending on how you're doing. I'd love to see that incorporated into scorev2. Personally, I think the best possible scoring system is a scoring system that has notes worth less or more, depending on how hard the map is at that point. This is probably unrealistic since this would need a good way to measure difficulty, and star rating has proven itself to not be very good, especially at harder maps. Still could be interesting to try IDK.
Grades in mania are based on acc because mania IS all about acc. And yes, adding combo to the score calculation is indeed a bad idea especially during tournaments where you only have 1 try. It's way too luck based.
I really understand the idea of rewarding consistency and i support it, but you simply can't do it map by map. It would only make pp farming frustrating like in standard...
I really understand the idea of rewarding consistency and i support it, but you simply can't do it map by map. It would only make pp farming frustrating like in standard...
Unless you know, I dev like me submits a pull request for it and there is a backing to support the idea.Veracion wrote:
As i already said, it's highly unlikely that there will be an SSS added, since there is no equivalent in the other game modes.
Make score = acc. Score is arbitrary anyway, so it can be anything. Since it can be anything, make it accuracy. Problem solved.Cuber wrote:
Why are the grades even based on accuracy at all? If score is a measurement of performance in a map, obviously the grading should be based on that and that alone! All grades do in my mind anyways is provide goals that feel more real than reaching an arbitrary number. On this train of thought, PP should also be entirely based on song difficulty and score.
They added combo to tournaments because the results were to close for their comfort back in 2016. Their line of thought was to intensify any discrete imperfections a player may have in a play and to prevent a decided result mid map for better spectating experience. They failed to realize they needed to at least adjust the scale (zoom into a score range) so that more experienced player's scores had further distance between them rather than cherry pick misses. They also failed to realize that they cannot artificially create an undecided result mid map and have the score mirror the skill a player has. That is not skill but randomness.LastExceed wrote:
. And yes, adding combo to the score calculation is indeed a bad idea especially during tournaments where you only have 1 try. It's way too luck based.
The best way to go is how SM's new score system works, which is the system I proposed in my OD thread a while back. Have non discrete, continuous acc-score following a bell curve related to hit timing.
Ofc there is an argument about 65% FC VS 98% with a high miss-hit ratio, but there is no clear cut answer to which is more impressive.
I think that an SS is deserved when you don't get 200s AND that you have a proper ratio between 300 and 300g, like 1:10 or 1:8. Ah full 300g already has a value : 1 000 000 score and first rank. We don't need to put SS on top of it.
S < SS < 1 000 000
S < SS < 1 000 000
this part is obviousAdri wrote:
S < SS < 1 000 000
i disagree with that part, all 300 is hard enough imoAdri wrote:
I think that an SS is deserved when you don't get 200s AND that you have a proper ratio between 300 and 300g, like 1:10 or 1:8.
All 300 is hard but an SS should be the exception, a really good play. It doesn't have to be impossible tho, that is why we should have a ratio.
IMO mania is about being good at mania, and being good at mania should be represented by score. (I mention below why pure acc isn't a good representation of performance.)LastExceed wrote:
Grades in mania are based on acc because mania IS all about acc. And yes, adding combo to the score calculation is indeed a bad idea especially during tournaments where you only have 1 try. It's way too luck based.
I really understand the idea of rewarding consistency and i support it, but you simply can't do it map by map. It would only make pp farming frustrating like in standard...
Thinking about tournaments specifically doesn't really make sense to me. Why would a measure of performance differ on the situation around the play? I, like any reasonable person, am against a scoring system like standard for mania, that gravely punishes players for 1 mess up. The ideal scoring system (other than the unreasonable idea I mentioned in my earlier post) is a system that rewards consistency, but less than accuracy.
I'm confused by what you mean of figuring out consistency map by map. Could you please clarify?
Pure accuracy is not a good scoring system, because it does not reward consistency, which is an important part of skill. For example, an otherwise SS play with 2 misses at the same time is more impressive than an otherwise SS play with 2 misses spread out in the map. Obviously, in this example, the difference isn't huge, but still, score should represent performance on a map, and I stand with my position that pure accuracy is not the way to do this.abraker wrote:
Make score = acc. Score is arbitrary anyway, so it can be anything. Since it can be anything, make it accuracy. Problem solved.Cuber wrote:
Why are the grades even based on accuracy at all? If score is a measurement of performance in a map, obviously the grading should be based on that and that alone! All grades do in my mind anyways is provide goals that feel more real than reaching an arbitrary number. On this train of thought, PP should also be entirely based on song difficulty and score.
While writing this, I came up with a (probably stupid) idea. The reason I'm not a fan of using combo for consistency is because it is possible to mash through hard patterns and keep combo. Also, I don't think that 1 miss should affect score too much. I mentioned that I like the system of using bonus score. Why don't we make the worth of a note (at least in the consistency portion of score) equal (scaled appropiately obviously) to your current health? Obviously, changes to health would need to be done, to punish any judgement less than a 300. However, maybe with a bunch of tuning, this might work. I'm probably just an idiot tho lol
Cuber wrote:
Pure accuracy is not a good scoring system, because it does not reward consistency, which is an important part of skill. For example, an otherwise SS play with 2 misses at the same time is more impressive than an otherwise SS play with 2 misses spread out in the map. Obviously, in this example, the difference isn't huge, but still, score should represent performance on a map, and I stand with my position that pure accuracy is not the way to do this.
abraker wrote:
Ofc there is an argument about 65% FC VS 98% with a high miss-hit ratio, but there is no clear cut answer to which is more impressive
Jeez that's just adding onto like frankenstein. This can be mitigated if the acc curve were a bit steeper such that a 99% would be considered as hard as the combo+acc equivalent you have in mind. By making the acc curve steeper, you are intensifying areas where the player is likely to do poor on or miss, much like combo without the shit combo based scoring comes with. And there is no need to adjust miss windows unless you think current ones need adjusting.Cuber wrote:
While writing this, I came up with a (probably stupid) idea. The reason I'm not a fan of using combo for consistency is because it is possible to mash through hard patterns and keep combo. Also, I don't think that 1 miss should affect score too much. I mentioned that I like the system of using bonus score. Why don't we make the worth of a note (at least in the consistency portion of score) equal (scaled appropiately obviously) to your current health? Obviously, changes to health would need to be done, to punish any judgement less than a 300. However, maybe with a bunch of tuning, this might work. I'm probably just an idiot tho lol
By "making the accuracy curve steeper", do you mean we should lose more accuracy for a miss/50/100/200, or do you mean that we should lose more accuracy for a miss as we miss more (e.g., the second miss is more hurtful than the first)?
lose more accuracy for a miss/50/100/200. And berfore anyone cries, while it's like HR/higher OD, this adjustment should be independent of what the miss window is (don't change miss window when adjusting this).johnmedina999 wrote:
By "making the accuracy curve steeper", do you mean we should lose more accuracy for a miss/50/100/200, or do you mean that we should lose more accuracy for a miss as we miss more (e.g., the second miss is more hurtful than the first)?
If you convert acc to score out of 1M as it is right now, 960,000 and 990,000 (96% and 99%) will be a very small gap and is also where most decent plays fall to. Transforming that same gap to 650,000 and 990,000 would allow to highlight skill more clearly. Yes anyone who gets less than an S gets wrecked, but then again you shouldn't be surprised at such results when you play maps out of your skill range.
Uhm sorry, but I still doubt they would even consider it.abraker wrote:
Unless you know, I dev like me submits a pull request for it and there is a backing to support the idea.Veracion wrote:
As i already said, it's highly unlikely that there will be an SSS added, since there is no equivalent in the other game modes.
Interesting suggestion, that doesn't seem too bad cause it'd cause people to learn patterns better. Seems to be getting in the direction of bms / stepmania, where accuracy is more important than osu!mania's current system.abraker wrote:
If you convert acc to score out of 1M as it is right now, 960,000 and 990,000 (96% and 99%) will be a very small gap and is also where most decent plays fall to. Transforming that same gap to 650,000 and 990,000 would allow to highlight skill more clearly. Yes anyone who gets less than an S gets wrecked, but then again you shouldn't be surprised at such results when you play maps out of your skill range.
Maybe the scoring shouldn't be to that extend, but it doesn't seem to be a bad direction. Maybe then less people would complain about smashing maps on an A.
Would time to get used to it though.
lmao yes.Veracion wrote:
only slightly less playing experience than the people developing scorev2 xdVeracion wrote:
only slightly less playing experience than the people developing scorev2 xd
hahaha good one
I have some ideas of how to improve the current scoreV2. Nearly nobody in the mania community likes the direction of this scoring system, and many good arguments have been made for why this scoring system and bad and why another scoring system would be better. However, especially now with the knowledge that osu!lazer will bring custom gamemodes, it makes sense for the osu!mania scoring system to employ a scoring system that fits into the pattern with the scoreV2 in other gamemodes. Those who want to play a gamemode with their favorite scoring system are welcome to.
That being said, here are some of my opinions on how to improve the current iteration of osu!mania scoreV2.
I hope that my suggestions are considered.
That being said, here are some of my opinions on how to improve the current iteration of osu!mania scoreV2.
Combo:
I don't quite understand why hit score is factored into this at all, isn't that the point of the accuracy portion of score? Also, there are the oddities of losing differents amounts of score for a non-perfect judgment, depending on what combo you had at the time. Only taking into account the combo, and not the hit score, would solve this problem.
I think it is too easy to spam through hard sections and hold combo. Making 50s (and maybe 100s) break combo would help. After all, combo is a number that tracks the number of notes that you haven't messed up on, and I would call getting a 50 a mess up.
Lastly, I think that as an anti-spam mechanic, hitting more keys than needed (not between notes, only for notes) should break combo.
I don't quite understand why hit score is factored into this at all, isn't that the point of the accuracy portion of score? Also, there are the oddities of losing differents amounts of score for a non-perfect judgment, depending on what combo you had at the time. Only taking into account the combo, and not the hit score, would solve this problem.
I think it is too easy to spam through hard sections and hold combo. Making 50s (and maybe 100s) break combo would help. After all, combo is a number that tracks the number of notes that you haven't messed up on, and I would call getting a 50 a mess up.
Lastly, I think that as an anti-spam mechanic, hitting more keys than needed (not between notes, only for notes) should break combo.
Misc:
I know this isn't super relevant here, but please make grades based off score, not accuracy. If score is how you assess the performance of a play, use that for the grade.
I know this isn't super relevant here, but please make grades based off score, not accuracy. If score is how you assess the performance of a play, use that for the grade.
I hope that my suggestions are considered.
+1Cuber wrote:
I know this isn't super relevant here, but please make grades based off score, not accuracy. If score is how you assess the performance of a play, use that for the grade.
One of the reasons why SS makes no sense is this
yeah and you can finally use the "sorted by ranking" because now i can use it and have tons of S with 900k+ and 700k+ scores who are worth nothing and i still need to search for bad scores :/
I was so relieved when i read thisSmoogipooo (on reddit) wrote:
Combo scoring: I don't remember if I mentioned this publicly (I thought I did but can't find the post), but I want to try accuracy-only scoring.
source
I went back a few pages in this thread and I haven't seen this yet, so I'm gonna go ahead and try to give an objective opinion about the current scoreV2:
LN change
This part turned out VERY good. I haven't seen a single player who dislikes it yet. The way it is now makes perfectly sense, and I especially like the 1.5x tolerance of releases since those are indeed very hard to time. Even though combo will (hopefully) be meaningless, I do think it was a good idea to remove the crazy amount of combo you get from LNs, especially if HD and FI stay scaling to combo. This brings us to the next topic:
Mods and multipliers
In this topic there's alot of different things to look at: lets start with multipliers. First of all: VMs being back to x1.0 is a good thing. There is too many people who use HD or FL by preference, and even though I am currently the only one doing the same with FI i do think that one should stay x1.0 as well.
Next: DT/NC. I don't quite know how this one works at the moment, but it feels like its simply the same as NoMod except that PP is calculated with the increased StarRating ect. (correct me if im wrong). DT PP brought back alot of players that moved to StepMania/BMS/O2Jam/idkwhatelse because osu!mania didn't have enough hard maps. Yes, the DT scores are currently giving way too much PP, but this actually isn't the fault of DT but the fault of the StarRating system which heavily overrates double trills. (2 days after DT PP was released peppy said it will be nerfed after several 2k+ scores were set. Please dont do that). Nerfing DT PP would therefore be a bad idea since maps that aren't overrated wouldnt give any DT PP at all anymore. If you're planning to change something in here, fix the SR system. Doubletrills need to be nerfed, and rice needs to be buffed (have a look at empress [SC], which is currently the most underrated ranked map).
Idk how osu!standard works in this aspect, but I don't think a multiplier would make sense on DT/NC, since you can't compare NoMod scores with DT scores anyway.
About HR: I interested in why it is currently UNRANKED instead of x1.0 because I can't see how it could be abused. HR is something that should definitely be a thing, though idk which multiplier.
Random/Mirror: Random should stay unranked, because it can be abused (1handed patterns can be turned into 2 handed patterns and vice versa). But a mirror mod (in case it will ever be a thing) would be a blessing to left handed players, because some maps are very right-based (onbeat notes are right hand, offbeat left hand all the time which is very mindblocking). It even goes so far that some players actually switch their scroll direction and rotate their monitor by 180° to achieve the same effect.
Autoconverts and keymodes: Autoconverts never give a noteworthy amount of PP so its pretty irrelevant, but I dislike that changing your amount of keys (no matter if increasing or decreasing) decreases your multiplier. The key modes should be split up into separated rankings instead.
HalfTime: I don't know if this was ever addressed before, but something definitely needs to change in here. First of all: HT gives too much PP. Idk why but it does. I think that instead of halving the score, it should work the same way DT does (identical calcultion with just the decreased SR ect).
NoFail: This is something that in my opinion works with all gamemodes: NoFail should be x1.0, but UNRANKED. You shouldn't be able to be rewarded for blindly mashing through a crazy hard map.
Easy: Just like in osu!standard, this is a difficult topic. The main problem is: atm nobody uses it because instead of EZ you can pick HT which has the same multiplier but is way easier. If my suggestion to HT is applied then it could keep going with simply a multiplier below 1.0, execpt that x0.5 is too extreme. Unlike standard, you can't make up for that by holding combo since mania is acc based and has a linear score curve. i'd try going with something like x0.7 and see how that turns out.
SuddenDeath/Perfect: I don't think these need to be discussed.
Next: DT/NC. I don't quite know how this one works at the moment, but it feels like its simply the same as NoMod except that PP is calculated with the increased StarRating ect. (correct me if im wrong). DT PP brought back alot of players that moved to StepMania/BMS/O2Jam/idkwhatelse because osu!mania didn't have enough hard maps. Yes, the DT scores are currently giving way too much PP, but this actually isn't the fault of DT but the fault of the StarRating system which heavily overrates double trills. (2 days after DT PP was released peppy said it will be nerfed after several 2k+ scores were set. Please dont do that). Nerfing DT PP would therefore be a bad idea since maps that aren't overrated wouldnt give any DT PP at all anymore. If you're planning to change something in here, fix the SR system. Doubletrills need to be nerfed, and rice needs to be buffed (have a look at empress [SC], which is currently the most underrated ranked map).
Idk how osu!standard works in this aspect, but I don't think a multiplier would make sense on DT/NC, since you can't compare NoMod scores with DT scores anyway.
About HR: I interested in why it is currently UNRANKED instead of x1.0 because I can't see how it could be abused. HR is something that should definitely be a thing, though idk which multiplier.
Random/Mirror: Random should stay unranked, because it can be abused (1handed patterns can be turned into 2 handed patterns and vice versa). But a mirror mod (in case it will ever be a thing) would be a blessing to left handed players, because some maps are very right-based (onbeat notes are right hand, offbeat left hand all the time which is very mindblocking). It even goes so far that some players actually switch their scroll direction and rotate their monitor by 180° to achieve the same effect.
Autoconverts and keymodes: Autoconverts never give a noteworthy amount of PP so its pretty irrelevant, but I dislike that changing your amount of keys (no matter if increasing or decreasing) decreases your multiplier. The key modes should be split up into separated rankings instead.
HalfTime: I don't know if this was ever addressed before, but something definitely needs to change in here. First of all: HT gives too much PP. Idk why but it does. I think that instead of halving the score, it should work the same way DT does (identical calcultion with just the decreased SR ect).
NoFail: This is something that in my opinion works with all gamemodes: NoFail should be x1.0, but UNRANKED. You shouldn't be able to be rewarded for blindly mashing through a crazy hard map.
Easy: Just like in osu!standard, this is a difficult topic. The main problem is: atm nobody uses it because instead of EZ you can pick HT which has the same multiplier but is way easier. If my suggestion to HT is applied then it could keep going with simply a multiplier below 1.0, execpt that x0.5 is too extreme. Unlike standard, you can't make up for that by holding combo since mania is acc based and has a linear score curve. i'd try going with something like x0.7 and see how that turns out.
SuddenDeath/Perfect: I don't think these need to be discussed.
300 & 300r
although i have a very bad acc compared to other players on my level (which means i suffer alot from this change), I do think it is a good idea to decrease 300's to 60/61 (~98.36)%. It makes sense and also solves the problem of top tier players having 99.xx % EVERYWHERE. Some players aren't even able to pass a map without getting an S since they are so accurate. Having everything decreased a bit would be a good thing. There's just one thing im afraid of: If the PP system stays unchanged in this aspect then a better performance is required on the same map to gain the same, which would be a big problem to low acc passes. The one thing i like most about mania is the fact that you are rewarded for how good you play in general. Even a barely-pass with horrible acc can be your top score if its done on a map that is very hard for your standards and I really want to keep this.
combo
Here we are, at the most controversial topic of them all. I don't even know what to say about it at this point. I don't want mania to become frustrating like standard. Right now when you miss a note in mania, it drops your acc a little and thats pretty much it. While in standard, if you miss a note then your score is instantly worthless. I'm not going into detail about how stupid i find that since this thread is about mania, but I do want to say: PLEASE DON'T DO THIS TO MANIA! I want mania to be acc only (In my opinion you could even go so far to completely remove score and use acc for scoreboards) and I am sure many players (especially those who came from other VSRGs) will agree with this.
SV changes
Here comes something completely new: Would it be possible to add SVs to the SR calculation system? I know it's going to be hard to make this system unabusable (so that invisible notes ect don't lead to infinite SR ect) but I have faith in the developers to be capable of making it happen. But before that, I'd like to hear some opinions on this.
If SS is based on 1 000 000 score, hardly anyone would get an SS on anything past 4*, and past 5* it would be virtually impossible.Adri wrote:
+1Cuber wrote:
I know this isn't super relevant here, but please make grades based off score, not accuracy. If score is how you assess the performance of a play, use that for the grade.
One of the reasons why SS makes no sense is this
And if it's not based on 1 000 000 (say it's based on 990 000 or something similar), keep in mind that accuracy now decreases with 300 compared to 300g, just as you get less score with 300 as opposed to 300g. Accuracy affects score, so minuscule mistakes would be a lot more punishing than before.
The only way grades based on score would work is if score is 100% based on accuracy (like DDR), and even then the grades would be based on accuracy by extension.
why not just keep the SS requirement at "300 and 300r only" as it is right now?
That's what I'm saying. Cuber's idea would either go with this or completely destroy it, depending on what the SS requirement is.LastExceed wrote:
why not just keep the SS requirement at "300 and 300r only" as it is right now?
But again, you lose accuracy now with 300, so the accuracy SS requirement would have to be adjusted.
you got it wrong. My idea is to make SS completely unrelated to acc. As long as you have 300 and 300r only you get the SS no matter your acc. which means you could theoretically get an SS with 98.36% (everything 300 and no 300r)johnmedina999 wrote:
But again, you lose accuracy now with 300, so the accuracy SS requirement would have to be adjusted.
LastExceed wrote:
you got it wrong. My idea is to make SS completely unrelated to acc. As long as you have 300 and 300r only you get the SS no matter your acc. which means you could theoretically get an SS with 98.36% (everything 300 and no 300r)
Ah, I see. Yeah, that works.
Basically what I mean is that accuracy should be 100% entirely completely fully wholly irrelevant. In everything (except for contributing to score).johnmedina999 wrote:
If SS is based on 1 000 000 score, hardly anyone would get an SS on anything past 4*, and past 5* it would be virtually impossible.
And if it's not based on 1 000 000 (say it's based on 990 000 or something similar), keep in mind that accuracy now decreases with 300 compared to 300g, just as you get less score with 300 as opposed to 300g. Accuracy affects score, so minuscule mistakes would be a lot more punishing than before.
The only way grades based on score would work is if score is 100% based on accuracy (like DDR), and even then the grades would be based on accuracy by extension.
However, everything you guys are talking about is unrelated to ScoreV2. I'd appreciate someone giving their thoughts on my ideas (or any other ideas) on the more relevant aspects of ScoreV2.
please separate SS from 100% and make it reliant on having 100% 300g + 300g; you can keep the reduction of accuracy percentage for getting regular 300s as it stands right now, but having to say "score v2 SS" is absolutely obnoxious
also, add SSS rank for 1m point scores; they are rare and few/far-between, but they do in fact exist
other than that: watching score v2 in tournament play for the past few weeks has shown that it is a much more viable system than it was in the past and I think it's certainly working
i personally like Cuber's idea of making grades related to score, so long as there are no instances where a SS grade can be higher than a S grade using the near impossible example of getting regular 300 judgment for every single note, as i do feel like SS rank should be something that is conditional much like older DDR was for getting AAAs (USA's DDR Extreme CS had a condition that AAs were only possible if you FC'd due to bonus points, that's not as good of an example though)
also, add SSS rank for 1m point scores; they are rare and few/far-between, but they do in fact exist
other than that: watching score v2 in tournament play for the past few weeks has shown that it is a much more viable system than it was in the past and I think it's certainly working
i personally like Cuber's idea of making grades related to score, so long as there are no instances where a SS grade can be higher than a S grade using the near impossible example of getting regular 300 judgment for every single note, as i do feel like SS rank should be something that is conditional much like older DDR was for getting AAAs (USA's DDR Extreme CS had a condition that AAs were only possible if you FC'd due to bonus points, that's not as good of an example though)
Honestly the ratio of combo to accuracy in score should be 0% to 100%. When I get a 96% on a map and its still a lower score than a 91% that's just stupid. Oh yeah and visual mods shouldn't give increased score, I know people who ONLY play with them, and are actually worse without them.
out of curiousity, why do compare the score to accuracy? do you think that accuracy is the perfect scoring system?tatatat wrote:
Honestly the ratio of combo to accuracy in score should be 0% to 100%. When I get a 96% on a map and its still a lower score than a 91% that's just stupid. Oh yeah and visual mods shouldn't give increased score, I know people who ONLY play with them, and are actually worse without them.
Those who prefer accuracy over combo don't care as much for the consistency element. Only frustration comes out of retrying so often to get a perfect run. It's better to just do the same when attempting that 99.9X% whenever you are ready for it instead of retrying it over 1000 times until you get that 80% FC.Cuber wrote:
out of curiousity, why do compare the score to accuracy? do you think that accuracy is the perfect scoring system?tatatat wrote:
Honestly the ratio of combo to accuracy in score should be 0% to 100%. When I get a 96% on a map and its still a lower score than a 91% that's just stupid. Oh yeah and visual mods shouldn't give increased score, I know people who ONLY play with them, and are actually worse without them.
Do we have a date when this is going to roll out? Is it going to roll out with osu laser?
It needs more work tbhjohnmedina999 wrote:
Do we have a date when this is going to roll out? Is it going to roll out with osu laser?