Kudos to Agka for making the first SV Guide thread and huge thanks for the SV tool, but personally felt that it can be simplified further so here it is
Another guide that is less layman by Agka
A very useful SV tool by Agka (Recommended only if you know what's going on on this post)
I APOLOGIZE FOR THE HORRIBLE ILLUSTRATIONS IN ADVANCE THOUGH I STUDY ART BUT I CAN'T DRAW
EDIT: OK THIS LOOKS BETTER THAN EXPECTED, COOL
--
ANALOGICAL GUIDE
We can start off with a really simple analogy on how an SV change works:
DISTANCE
The distance we want to use, we will just quantify this by the number of white lines you pass through:

You can quantify this distance by the number of blue lines it passes through and the results will still be the same
Take note that 3 + 1/2 means 3 + 0.5 NOT (3+1)/2
For explaning purposes, we use the analogy that the distance is how big a cup is.
Basically if your distance is 1000 White Lines you HAVE A HUGE FUCKING CUP
SV A.K.A VROOM SPEED
The SV is basically the number you put in the green line thing, if you don't know what's a green line/SV idk why you reading this
Note: Your SV is limited by the lower bound 0.1 and the upper bound 10, that means you can't go lower than 0.1 and higher than 10
For explaning purposes, we use the analogy that the SV is how fast you pour water into the cup
Basically if your SV is 10 you are pouring A FUCK-TON OF WATER VERY FAST
DISTANCE COVERED BY THE SV
NOT THE SAME AS DISTANCE
The distance covered by the SV is basically how long your SV is going to last ,we also quantify this as the number of white lines you pass through.

As you can see,
SV A will last 2 white lines
SV B will last 3/4 white lines
SV C will last 5/4 white lines
Take note that ALL distances covered by the SVs will always sum up to Distance
For example, for the image above, since the whole distance is 4 White Lines, we find that adding all distances covered by the SVs: 2 White Lines + 3/4 White Lines + 5/4 White Lines = 4 White Lines
For explaning purposes, we use the analogy that the distance covered by the SV is how long you plan to pour water into the cup
I probably don't need an example
--
With that all down, I present to you the formula:
∑(Distances covered by the SV * SV) = Amount of distance travelled
First Distance covered by the SV * First SV + Second Distance covered by the SV * Second SV + Third Distance covered by the SV * Third SV + ... = Amount of distance travelled
In analogical terms:
--
EXAMPLE ONE
We have a cup that is 4 White Lines big(Distance)
If you pour in water(First SV) at a unit of 2, for a duration of 2 White Lines (First Distance covered by the SV)
Then you pour in water again(Second SV) at a unit of 0.2, for a duration of 2 White Lines (Second Distance covered by the SV)
If we do the math on how much water you poured in the cup:
(First SV) * (First Distance covered by the SV) + (Second SV) * (Second Distance covered by the SV) = Amount of water poured
2 * 2 White Lines + 0.2 * 2 White Lines = 4.4 White Lines
Comparing it to the cup size, we can say it overflowed by 0.4 White lines, and this is the distance that the player will see as extra due to it being too fast(too full)
HENCE THIS SV APPEARS TO BE ON AVERAGE SLIGHTLY FASTER
--
EXAMPLE TWO
We have a cup that is 5.6 White Lines big(Distance)
If you pour in water(First SV) at a unit of 0.3, for a duration of 3.5 White Lines (First Distance covered by the SV)
Then you pour in water again(Second SV) at a unit of 2, for a duration of 2.1 White Lines (Second Distance covered by the SV)
If we do the math on how much water you poured in the cup:
(First SV) * (First Distance covered by the SV) + (Second SV) * (Second Distance covered by the SV) = Amount of water poured
0.3 * 3.5 White Lines + 2 * 2.1 White Lines = 5.25 White Lines
Comparing it to the cup size, we can say you didn't pour enough in it by 0.35 White lines, and this is the distance that the player will see cut off due to it being too slow(not filled)
HENCE THIS SV APPEARS TO BE ON AVERAGE SLIGHTLY SLOWER
--
EXAMPLE THREE
This is the way to make SVs have an average speed of 1.0 (this means that the distance between the SV appear to be the same with or without SVs)
We have a cup that is 3 White Lines big(Distance)
If you pour in water(First SV) at a unit of 0.5, for a duration of 1.0 White Lines (First Distance covered by the SV)
Then you pour in water again(Second SV) at a unit of X, for a duration of 2.0 White Lines (Second Distance covered by the SV)
If we do the math on how much water you poured in the cup:
(First SV) * (First Distance covered by the SV) + (Second SV) * (Second Distance covered by the SV) = Amount of water poured
0.5 * 1.0 White Lines + X * 2.0 White Lines = 3 White Lines
TAKE NOTE THAT IF WE WANT THE CUP TO NOT OVERFLOW THE AMOUNT OF WATER YOU POUR MUST BE EXACTLY 3 WHITE LINES IN THIS CASE
Solve for X and you should get 1.25, that is the value you should put for the Second SV
HENCE THIS SV DOESN'T APPEAR TOO FAST NOR SLOW
--
In Conclusion:
If you want to have an SV that is on average faster than usual, pour enough water so that it overflows
Vice versa
If you want to have an SV that doesn't affect original visual distance/gameplay/plays better, pour enough water so that it exactly fills to the brim
--
I said it was for beginners, I know there are some errors but this is good enough (hopefully) for people to understand how this works
IT'S LIKE I'M YELLING FOR THE WHOLE POST
DISTANCE
The distance we want to use, we will just quantify this by the number of white lines you pass through:
Take note that 3 + 1/2 means 3 + 0.5 NOT (3+1)/2
For explaning purposes, we use the analogy that the distance is how big a cup is.
Basically if your distance is 1000 White Lines you HAVE A HUGE FUCKING CUP
SV A.K.A VROOM SPEED
The SV is basically the number you put in the green line thing, if you don't know what's a green line/SV idk why you reading this
Note: Your SV is limited by the lower bound 0.1 and the upper bound 10, that means you can't go lower than 0.1 and higher than 10
For explaning purposes, we use the analogy that the SV is how fast you pour water into the cup
Basically if your SV is 10 you are pouring A FUCK-TON OF WATER VERY FAST
DISTANCE COVERED BY THE SV
NOT THE SAME AS DISTANCE
The distance covered by the SV is basically how long your SV is going to last ,we also quantify this as the number of white lines you pass through.
SV A will last 2 white lines
SV B will last 3/4 white lines
SV C will last 5/4 white lines
Take note that ALL distances covered by the SVs will always sum up to Distance
For example, for the image above, since the whole distance is 4 White Lines, we find that adding all distances covered by the SVs: 2 White Lines + 3/4 White Lines + 5/4 White Lines = 4 White Lines
For explaning purposes, we use the analogy that the distance covered by the SV is how long you plan to pour water into the cup
I probably don't need an example
--
With that all down, I present to you the formula:
First Distance covered by the SV * First SV + Second Distance covered by the SV * Second SV + Third Distance covered by the SV * Third SV + ... = Amount of distance travelled
In analogical terms:
--
EXAMPLE ONE
We have a cup that is 4 White Lines big(Distance)
If you pour in water(First SV) at a unit of 2, for a duration of 2 White Lines (First Distance covered by the SV)
Then you pour in water again(Second SV) at a unit of 0.2, for a duration of 2 White Lines (Second Distance covered by the SV)
If we do the math on how much water you poured in the cup:
(First SV) * (First Distance covered by the SV) + (Second SV) * (Second Distance covered by the SV) = Amount of water poured
2 * 2 White Lines + 0.2 * 2 White Lines = 4.4 White Lines
Comparing it to the cup size, we can say it overflowed by 0.4 White lines, and this is the distance that the player will see as extra due to it being too fast(too full)
--
EXAMPLE TWO
We have a cup that is 5.6 White Lines big(Distance)
If you pour in water(First SV) at a unit of 0.3, for a duration of 3.5 White Lines (First Distance covered by the SV)
Then you pour in water again(Second SV) at a unit of 2, for a duration of 2.1 White Lines (Second Distance covered by the SV)
If we do the math on how much water you poured in the cup:
(First SV) * (First Distance covered by the SV) + (Second SV) * (Second Distance covered by the SV) = Amount of water poured
0.3 * 3.5 White Lines + 2 * 2.1 White Lines = 5.25 White Lines
Comparing it to the cup size, we can say you didn't pour enough in it by 0.35 White lines, and this is the distance that the player will see cut off due to it being too slow(not filled)
--
EXAMPLE THREE
This is the way to make SVs have an average speed of 1.0 (this means that the distance between the SV appear to be the same with or without SVs)
We have a cup that is 3 White Lines big(Distance)
If you pour in water(First SV) at a unit of 0.5, for a duration of 1.0 White Lines (First Distance covered by the SV)
Then you pour in water again(Second SV) at a unit of X, for a duration of 2.0 White Lines (Second Distance covered by the SV)
If we do the math on how much water you poured in the cup:
(First SV) * (First Distance covered by the SV) + (Second SV) * (Second Distance covered by the SV) = Amount of water poured
0.5 * 1.0 White Lines + X * 2.0 White Lines = 3 White Lines
TAKE NOTE THAT IF WE WANT THE CUP TO NOT OVERFLOW THE AMOUNT OF WATER YOU POUR MUST BE EXACTLY 3 WHITE LINES IN THIS CASE
Solve for X and you should get 1.25, that is the value you should put for the Second SV
--
In Conclusion:
If you want to have an SV that is on average faster than usual, pour enough water so that it overflows
Vice versa
If you want to have an SV that doesn't affect original visual distance/gameplay/plays better, pour enough water so that it exactly fills to the brim
--
I said it was for beginners, I know there are some errors but this is good enough (hopefully) for people to understand how this works
GRAPHICAL GUIDE
HOW WE QUANTIFY DISTANCES
The distance we want to use, we will just quantify this by the number of white lines you pass through:

You can quantify this distance by the number of blue lines it passes through and the results will still be the same
Take note that 3 + 1/2 means 3 + 0.5 NOT (3+1)/2
HOW WE QUANTIFY DISTANCE COVERED BY THE SV
The distance covered by the SV is basically how long your SV is going to last ,we also quantify this as the number of white lines you pass through.

As you can see,
SV A will last 2 white lines
SV B will last 3/4 white lines
SV C will last 5/4 white lines
Take note that ALL distances covered by the SVs will always sum up to distance bounded by the first and last SV
For example, for the image above, since the whole distance is 4 White Lines, we find that adding all distances covered by the SVs: 2 White Lines + 3/4 White Lines + 5/4 White Lines = 4 White Lines
SV, the distance covered by SV, and distance traveled is related by the equation of:
∑(Distances covered by the SV * SV) = Amount of distance traveled
With that we can interpret this in the form of a graph where:
y-axis: SV (Speed)
x-axis: Distances covered by the SV (Time)
Area under the graph: Amount of distance traveled (Distance)
Take note to not confuse x-axis and Area under the graph, we use this graph as most of the time we are just finding the area under the graph
This is what a Speed against Time graph will look like if you only had a 1.0 SV (default) for your whole map:
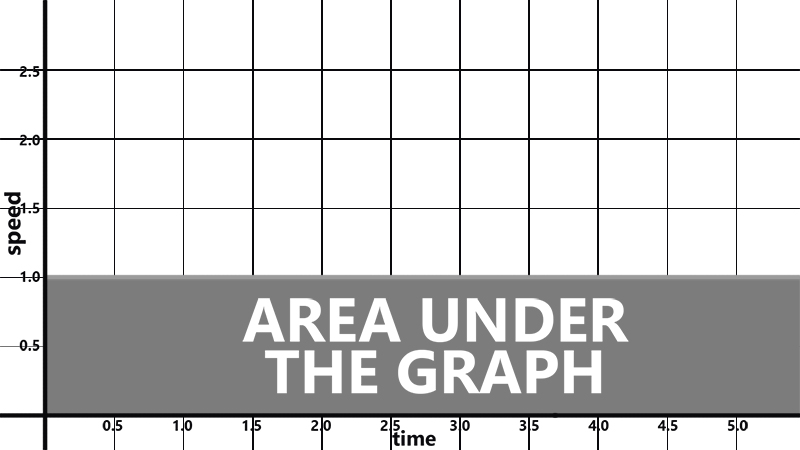
Important note:
In order to have a series of SV that averages on 1.0x SV (this makes it sightreadable most of the time), we need to make sure that:
MODIFIED AREA UNDER THE GRAPH = ORIGINAL AREA UNDER THE GRAPH
Modified area under the graph is the area under the graph when you put in SVs
Original area under the graph is the area under the graph when you DON'T put in any SV (means 1.0 SV throughout)
Now we can look at some examples to further your understanding:
EXAMPLE
Lets say we have 4 sets of values:
Take note:
y-axis: SV (Speed)
x-axis: Distances covered by the SV (Time)
Area under the graph: Amount of distance travelled (Distance)
Data₁ : { Speed₁ = 1.5, Time₁ = 1 White Line }
Data₂ : { Speed₂ = 0.8, Time₂ = 3 White Lines }
We can graph it like this:
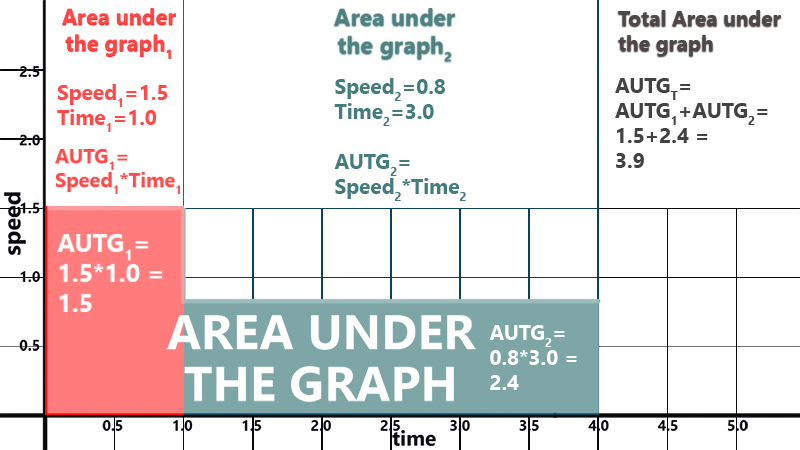
AUTG: Area Under The Graph
We can then calculate the modified area under the graph using simple geometrical calculations:
1.5 * 1 White Line + 0.8 * 3 White Lines = 3.9 White Lines (This is the modified area under the graph)
Then we calculate the original area under the graph (if all Speeds are 1.0):
1.0 * 1 White Line + 1.0 * 3 White Lines = 4.0 White Lines (This is the original area under the graph)
--
We can see that MODIFIED AREA UNDER THE GRAPH < ORIGINAL AREA UNDER THE GRAPH:
This we can say that when the SV is in effect, players will feel that the SV here is slower than expected on average
--
IF you calculated that MODIFIED AREA UNDER THE GRAPH > ORIGINAL AREA UNDER THE GRAPH:
This we can say that when the SV is in effect, players will feel that the SV here is faster than expected on average
--
IF you calculated that MODIFIED AREA UNDER THE GRAPH = ORIGINAL AREA UNDER THE GRAPH:
This we can say that when the SV is in effect, players will feel that the SV here isn't faster nor slower than expected on average (this is the ideal result we want if we want sightreadable SVs (take note that this doesn't work 100% but it works MOST of the time)
The distance we want to use, we will just quantify this by the number of white lines you pass through:
Take note that 3 + 1/2 means 3 + 0.5 NOT (3+1)/2
HOW WE QUANTIFY DISTANCE COVERED BY THE SV
The distance covered by the SV is basically how long your SV is going to last ,we also quantify this as the number of white lines you pass through.
SV A will last 2 white lines
SV B will last 3/4 white lines
SV C will last 5/4 white lines
Take note that ALL distances covered by the SVs will always sum up to distance bounded by the first and last SV
For example, for the image above, since the whole distance is 4 White Lines, we find that adding all distances covered by the SVs: 2 White Lines + 3/4 White Lines + 5/4 White Lines = 4 White Lines
SV, the distance covered by SV, and distance traveled is related by the equation of:
∑(Distances covered by the SV * SV) = Amount of distance traveled
With that we can interpret this in the form of a graph where:
y-axis: SV (Speed)
x-axis: Distances covered by the SV (Time)
Area under the graph: Amount of distance traveled (Distance)
Take note to not confuse x-axis and Area under the graph, we use this graph as most of the time we are just finding the area under the graph
This is what a Speed against Time graph will look like if you only had a 1.0 SV (default) for your whole map:
Important note:
In order to have a series of SV that averages on 1.0x SV (this makes it sightreadable most of the time), we need to make sure that:
Modified area under the graph is the area under the graph when you put in SVs
Original area under the graph is the area under the graph when you DON'T put in any SV (means 1.0 SV throughout)
Now we can look at some examples to further your understanding:
EXAMPLE
Lets say we have 4 sets of values:
Take note:
y-axis: SV (Speed)
x-axis: Distances covered by the SV (Time)
Area under the graph: Amount of distance travelled (Distance)
Data₁ : { Speed₁ = 1.5, Time₁ = 1 White Line }
Data₂ : { Speed₂ = 0.8, Time₂ = 3 White Lines }
We can graph it like this:
We can then calculate the modified area under the graph using simple geometrical calculations:
1.5 * 1 White Line + 0.8 * 3 White Lines = 3.9 White Lines (This is the modified area under the graph)
Then we calculate the original area under the graph (if all Speeds are 1.0):
1.0 * 1 White Line + 1.0 * 3 White Lines = 4.0 White Lines (This is the original area under the graph)
This we can say that when the SV is in effect, players will feel that the SV here is slower than expected on average
This we can say that when the SV is in effect, players will feel that the SV here is faster than expected on average
This we can say that when the SV is in effect, players will feel that the SV here isn't faster nor slower than expected on average (this is the ideal result we want if we want sightreadable SVs (take note that this doesn't work 100% but it works MOST of the time)

