forum
Order of Operations (Maths)
posted
Total Posts
15
Which order of operations is being used in your country?
Total votes: 23
Topic Starter
im am using pemdas rn in school
Karmine wrote:
What are these things.
I just use correct order lmao
This is what happens when twitter users don't use Order of operations.
Topic Starter
Applying BODMAS, that's the correct answer.Stomiks wrote:
This is what happens when twitter users don't use Order of operations.
Twitter user is not wrong here.
Aren't they all the same just different words
I know Gemdas is basically Pemdas but it generalizes and doesn't just use parenthesis but all the grouping symbols (brackets, braces, parenthesis)
I know Gemdas is basically Pemdas but it generalizes and doesn't just use parenthesis but all the grouping symbols (brackets, braces, parenthesis)
Topic Starter
here, all brackets are considered brackets and we attribute adjectives to the different types of brackets []=square brackets, ()=round brackets or just brackets, {}=curly brackets and <>=angular brackets.Yhuan Debeste wrote:
Aren't they all the same just different words
I know Gemdas is basically Pemdas but it generalizes and doesn't just use parenthesis but all the grouping symbols (brackets, braces, parenthesis)
That's just how we call them, in those countries where the term brackets is used at the start of the order of operations.
Most countries that use Pemdas were influenced by the US that uses a different term parenthesis.
I have no idea what any of the things you put mean but that equation does give 9
Topic Starter
The order in which you perform your maths calculations.Patatitta wrote:
I have no idea what any of the things you put mean but that equation does give 9
Here are two examples:-
BODMAS: Brackets, Of(Order), Division, Multiplication, Addition, Subtraction.
BIDMAS: Brackets, Indices, Division, Multiplication, Addition, Subtraction.
'Of' and 'Indices' refer to the power/exponent of the number.
Different countries explain this concept with different terms, but the idea is retained at the core. I'm not sure how every country teaches it.
looked at google and found we use pemdas
My 2 cent: the main problem is how it's visually created to made some ppl unknowingly/instictively group the 2 and the bracket together instead of doing in left-to-right order (since the multiply and divide formula are considered the same in priority), causing in ppl getting the result of 1 instead of 9.Stomiks wrote:
This is what happens when twitter users don't use Order of operations.
You can imagine a simpler equivalent:
12÷6×3
Doing normally from left to right would get the result of 6, but following some Twitter people you'll get 2/3 instead. That is because they essentially group the latter formula which can be demonstrated with brackets like this:
12÷(6×3)
However they forgot that by having divide symbol at the front of the group you have to switch all your multiply to divide as well, like the deal with minus/subtract. So the correct method would be like this:
12÷(6÷3)=12÷2=6
don't mind my wall of text I used to have a nearly absolute mark on 9th grade math and I'm still irritated by how much ppl messed this shit up
Topic Starter
Zelzatter Zero wrote:
My 2 cent: the main problem is how it's visually created to made some ppl unknowingly/instictively group the 2 and the bracket together instead of doing in left-to-right order (since the multiply and divide formula are considered the same in priority), causing in ppl getting the result of 1 instead of 9.Stomiks wrote:
This is what happens when twitter users don't use Order of operations.
You can imagine a simpler equivalent:
12÷6×3
Doing normally from left to right would get the result of 6, but following some Twitter people you'll get 2/3 instead. That is because they essentially group the latter formula which can be demonstrated with brackets like this:
12÷(6×3)
However they forgot that by having divide symbol at the front of the group you have to switch all your multiply to divide as well, like the deal with minus/subtract. So the correct method would be like this:
12÷(6÷3)=12÷2=6
don't mind my wall of text I used to have a nearly absolute mark on 9th grade math and I'm still irritated by how much ppl messed this shit up
However they forgot that by having divide symbol at the front of the group you have to switch all your multiply to divide as well, like the deal with minus/subtract. So the correct method would be like this:At first I was surprised on seeing this, I've never heard that division could cause the multiply symbol to change itself to divide, I was never taught this.
12÷(6÷3)=12÷2=6
So I went to enquire about this to a community where I could seek answers and this is what I got.
What do you have to say about this?
Maybe I'm blind but it seems that you did not put the original operation without the parentheses for people's reference, hence the confusion over why "the multiplication just decide to switch symbols".
Anyways back to the topic:
The last image pretty much sums up perfectly why even divisive symbol have to treat similarly to minus/subtract.
If you take the last line and demonstrate the fraction into one single line, you'll have this:
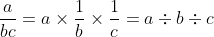
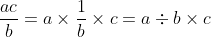
You can see apparently how the left one isn't the same as the original anymore. That also answer the statement of that image's author: They're not equal because they're not meant to be equal. The parentheses may confuse you but in this short scale of this operation, it's basically means you guys are doing it in the right-to-left order, not left-to-right, hence the debate on Twitter.
Anyways back to the topic:
The last image pretty much sums up perfectly why even divisive symbol have to treat similarly to minus/subtract.
If you take the last line and demonstrate the fraction into one single line, you'll have this:
You can see apparently how the left one isn't the same as the original anymore. That also answer the statement of that image's author: They're not equal because they're not meant to be equal. The parentheses may confuse you but in this short scale of this operation, it's basically means you guys are doing it in the right-to-left order, not left-to-right, hence the debate on Twitter.
Topic Starter
So it was my misunderstanding, thanks for clearing things up.Zelzatter Zero wrote:
Maybe I'm blind but it seems that you did not put the original operation without the parentheses for people's reference, hence the confusion over why "the multiplication just decide to switch symbols".