Note: I've thought about this idea for a while, and now with the recent touchscreen debacle I thought it was time to make a post about it. This isn't actually a solution to the TS issue, but it is relevant because it sparked a lot of debate about ways to change the current PP system. Read it on the new osu! website for better formatting.
What I see most people complain about with regards to the current PP system is how it fails to reward some skills (e.g. tech reading) and rewards other skills unfairly (e.g. aim). All these concerns can be summed up in one word: players want balance between skills. This here is a proposal that tries to do that automatically, with each skill rewarded proportional to the difficulty of attaining them.
I think this way of thinking about PP is the right way to go, but I can't guarantee that my preliminary version doesn't have flaws. My hope is just that if the osu!devs think it's worth the time, this system is tested on the database of scores that already exists, to see if it looks good and to check for weird cases. I can't do that myself because I don't have access to the database (except the top 100 plays on each map via the osu!api). Also, I don't want to pretend I have the definite solution to anything; Peppy and others will have much more experience thinking about this issue.
TL;DR: lol no, I'm not giving you a quick way out of this. Read the entire mind-bogglingly long thing. Also, there will be maths. :p
This here is approximately the history of osu! PP systems.
The complaints all seem to be some form of "the PP system does not weight X enough", where X can be skills like consistency, accuracy, sliders, tech reading, low-AR reading, etc.
And the proposed solutions to these complaints all seem to be some form of "weight skill X more". What I'm saying is that these kinds of solutions will never practically be sufficient, because we don't know exactly what kinds of skills being good at osu! requires, and we definitely don't know how to tell a computer what those skills are so that it can award PP based on them. So these types of solutions all seem to be a form of the typical error of applying specific solutions to a problem we can't specify.
The way to fix problems we can't specify is to offload the work of specifying the problem unto the solution itself. Yeah, uh, that was a confusing abstract garble of a sentence and I should start talking specifics.
PP!Balance is a twofold system, just like PPv2. First, the PP value of a play is calculated, then the PP from that play is added to your total PP with the same weightage system that PPv2 uses.
Here's the weightage system explained from the wiki entry (you can skip this if you already know).
The weightage system is necessary so that players can't gain more PP simply by setting more and more scores. If there were no weightage system in place, a player's PP would just be a measure of how many scores a player has set, not a measure of skill.
And how are the PP values for each play calculated?
The idea is that the PP of a play is supposed to measure how much better than others you are at that map. Call this the play's "Superiority". There are several ways to measure superiority of a play (e.g. rank achieved on map, percent score of top score, difference between the score and avg score and so on), and I talk about which way I think works best in the next section.
The essential difference between PP!Balance and PPv2 is that, unlike PPv2, PP!Balance doesn't try to directly define what it is exactly that is difficult in a beatmap (e.g. aim, accuracy, speed, reading, finger control, stamina and so on). Instead it lets the difficulty of a map be determined empirically by players' ability to play it.
If the hardest beatmap in the game is actually a lot more difficult than its low 5* rating suggests, you should get more PP for FCing it than for other maps of the same star rating. In fact, the ezpp! plugin tells me that you get 179pp and 201pp for SSing each of the maps respectively on the current PP system, so it does even worse worse than equal.
The PP system I'm proposing would give much more PP for FCing Scarlet Rose than the Veela map because FCing Scarlet Rose is very much better than most other players can do on the map. FCing the other map is still better than most, but it isn't as much better than an FC on Scarlet Rose is, so you won't get as much PP for it.
This also means that you can gain PP by being good at whatever you want, as long as there are ranked beatmaps for it. If you're not much better than others at aim, but you're still much better than others at tech reading, then you'll have an easier time gaining PP by playing tech maps than aim maps.
The players with the highest PP on this ranking system would then tend to be the players who are most better than others, which sounds sort of correct. In PPv2, the highest ranked players tend to be those who are best at a combination of aim, speed and accuracy, mostly ignoring other skills required to do well on beatmaps in osu!.
I will now proceed to cobble together the formula I think works best for calculating PP. I'm not sure this is the best formula possible. But instead of giving you my best suggestion first, I'm going to take you through some steps I personally went through in order to arrive at my best suggestion. I want to show you that there are options here, and I need to discuss them in order to explain why I think my latest version works best.
If you don't understand the technical details, you can still understand the system in broad strokes from the previous section and then give constructive feedback on it. No feedback is stupid (but pls don't yell at me).
So without further ado,
First idea: Rank-based superiority
My first thought was just, why not use the play's rank on the beatmap? If you get first place you get more PP than if you get 2nd place, and so on. We note that the difference in difficulty between the 1st and 2nd rank usually tends to be much greater than the difference in difficulty between the 101st and 102nd rank, so we conclude that there is something like a logarithmic distribution in the difficulty of attaining map ranks. Therefore the PP value of the scores should also scale logarithmically. We end up with something like this. (edit: Was PPv1 something similar? osu!wiki doesn't say.)

In the first term, N is the number of other plays made on that map (including your own plays and failed plays) set within 365 days past. The more plays-within-a-year a beatmap has, the more PP you get for getting a high score on it. The time limit is necessary to not unfairly disadvantage new maps that are just as hard as old maps but have fewer plays on them.
The reason why the PP of a play should depend on N is that the more people try a beatmap, the higher the competition is for getting high ranks on it. It is more difficult to win competitions where lots of other players compete, so you deserve more PP for ranking highly on them.
k is a constant weight that determines the importance of N. For example, say that k = 10,000. Then if you set a score on a beatmap with a 200,000 within-year play count, you multiply the play's PP value by 20. Or if the within-year play count was only 5,000, then you multiply the play's PP value by 0.5. It could also be that a different scaling of N works better.
The second term (1/ln(stuff)) is supposed to scale inversely logarithmically with your rank on a beatmap. Calculating for a few values of MapRank, we see that the PP value of 1st place gets multiplied by 1, 2nd place by 0.76, 101st by 0.2159, 102nd by 0.2154, and so on. It checks out.
(e-1 is there in the logarithm to make sure that the term equals 1 for MapRank = 1. If I instead wrote 1/ln(MapRank) without the e-1, then the term would equal 1/ln(1) when MapRank = 1. And since ln(1) = 0, you would have to divide by zero, and that is bad.)
The reason why I think this way of calculating PP is a bad idea is because on some maps, you see many players share the same score at the top, and it would be unfair to give different amounts of PP to players for exactly the same performance. And the corollary is that on other maps, the first ranks are arguably a lot better than any of the other scores, and this system isn't sensitive to degrees of superiority like that.
Second idea: ScoreV1-based superiority
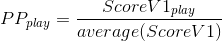
Take your score and divide it by the average score on that beatmap. If your score is exactly average, then PP_play = 1. If your score is 100 times greater than average, PP_play = 100. If your score is exactly half the average score, PP_play = 0.5. This system can then tell the difference between a score which is barely 1st place and a score which is way above what's needed for 1st place, and give PP accordingly. The idea assumes that average score on a beatmap is a good proxy for how difficult it is.
We can easily do some magic to make PP values range from 1 if the score is 100 times lower than average and 1000 if the score is 100 times greater than average. But the core idea is easier to represent with the simple equation above. We'll make the PP values have sensible ranges later.
It's probably wisest to take the average of all the top scores set by all players who have played the map (so if you play the map twice, only the top score gets counted when calculating the average). This is to prevent people from being able to purposefully set lots of bad scores on a map in order to drag down the average, making their top play worth more PP.
The main reason I think this system is insufficient is because it inherits the purposes and flaws of the current scoring system. A lot of players complain that accuracy has little effect on score, and indeed that would mean that accuracy has little effect on PP values in this system.
We have a few options here. The first option is to record all plays players make on maps, calculate what their ScoreV2 scores would be (even if they played using ScoreV1, we just recalculate using ScoreV2), and then do the PP!Balance calculations using those scores. Or we can invent a new scoring system and do the same with that. I prefer using ScoreV2, but you're free to argue why using something else is better.
Third idea: ScoreV2-based superiority
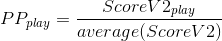
If a beatmap uses ScoreV1 for its leaderboards, then your top score on that leaderboard may not necessarily be the top PP play, because ScoreV1 and ScoreV2 is calculated differently. This is actually a problem with the current PP system, where you can make plays with a higher score but lower PP value, causing you to lose PP. If beatmap leaderboards will continue to stay ScoreV1, then I think the solution to this is just to keep two leaderboards for each beatmap, one for each scoring method, and then just make the ScoreV2 leaderboard hidden. That way, you can make plays that have a higher ScoreV1 value than ScoreV2 value without losing PP.
For the purposes of the PP calculations, the average score on the beatmap would then be the average of the hidden ScoreV2 leaderboard. If a player has played the beatmap twice, only their top ScoreV2 play gets counted into the average.
A problem with this way of doing it is that different maps have different HP values. For example, Airman has an HP of 3. This means that it will have a lot more bad scores than if the HP value was 7, dragging the average down considerably compared to maps with an HP value of 7. And since the average goes down, all the plays' PP values go up, making it easier to gain PP from maps with low HP value. And that's bad, because maps with lower HP values aren't necessarily harder than maps with higher HP values.
The solution seems to have to be some way of dealing with failed scores: the more failed scores a beatmap has, the more PP should be given. One way of dealing with this could be to just submit failed scores (i.e. their ScoreV2 values up until the point they failed) into a hidden database for that beatmap, and then include those scores when calculating the average score on that beatmap.
But this gives too much of an advantage to maps with high HP values. For example, I bet I'm not the only noob who has tried to play DoKito's Yomi Yori (HP = 6) several times only to fail horribly at the first stream. A large number of those plays would have gotten a much higher score if they were played on an identical beatmap with HP 4. Thus the HP 6 version would have had a lower average score if we add the failed scores.
So I think we need a more creative solution to the HP bar problem. EDIT 11/02/2018: The solution to this problem is really easy. (Thanks to Omnipotence -.) Just calculate the average score on a beatmap from the subset of the scores that would have passed if the beatmap had an HP value of 10. This way, the PP system treats all maps as if they had HP 10, so the actual HP value of a map won't affect the PP possible to gain from the map.
Another issue with this third idea is that some maps are popular for almost exclusively very new players, and other maps are popular for almost exclusively very good players. It will therefore be easier to do better than others on the former type of maps than on the latter type of maps.
Let's call this problem "differential popularity" (better players tend to play harder maps, less good players tend to play easier maps) so that it's easier to talk about. This is actually also a problem in the first and second ideas, and it makes it hard to reliably measure the real difficulty of beatmaps. (Edit: I wrote a section on solving this problem later in this post.)
Having explained why I think this is the way we should define PP values, we now turn to finding a way to make this formula have the proper range of values.
Defining the range
I think the difference in PP values of the worst play to the current best play should be something like a 1000 PP. A bit less or a bit more is fine. This is approximately the range of the current PP system. Maybe the new system should have slightly higher values because then the transition won't make many players angry about "losing" PP?
Anyway, here's the formula I think has the best scaling. I won't go into how I arrived at this equation, but if you need to know you can ask me.
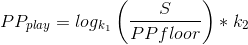
Where we define the S variable ("Superiority") with the formula from the previous section.
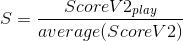
In other words, S is the ratio of the ScoreV2 value of your play and the average ScoreV2 values of all the plays on the dedicated ScoreV2 leaderboard (see the first paragraph in the previous section).
PPfloor is the lowest value of S we want to give PP to. We give 0 PP to all scores below it. I think plays that have an S value of less than 0.01 can safely be given 0 PP to, because I think even the newest players can find maps they can achieve an S of above 0.01 on (but if I'm wrong, we can set PPfloor even lower). Consider, in order to achieve an S of lower than 0.01, you must score (ScoreV2) something like 5,000 on maps that have an average score of 500,000. So PPfloor = 0.01 looks good to me.
k_1 and k_2 are constants that determine the range of PP values. If we set k_1 = 2.5 and k_2 = 100 then the range for different values of S looks like this.

To achieve 1256 PP, you need to score a thousand times better than average. For example by scoring 1,000,000 (nomod SS) on a map with average score of 1,000. You can fiddle with the constants in this Google spreadsheet to see what they do (anyone with link can edit).
I'm not sure what the best weighting is. I think the way to find out is to set the weights to something and then use the formula to calculate a bunch of PP values from plays that have already been set, and see if it the results look about right.
Also, I think it'd make sense to not give plays on a map PP before at least a thousand players have set scores on the map. Otherwise the PP values of the plays would be too dependent on random initial conditions.
Imagine I set the number one score on xi - FREEDOM DiVE [FOUR DIMENSIONS] (normal score for me tbh). A HDHR SS worth 1,120,000 points on ScoreV2. Let's also say that the average ScoreV2 on that beatmap is 100,000 (I have no idea). So that gives us an S of 11.2. Assume we use the same weighting of the constants as I gave them in the section on "Defining the range".
The amount of PP I would get would then be...
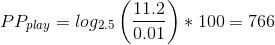
In any PP system that tries to directly define what "difficulty" is (e.g. by defining it as a function of aim, speed, accuracy and strain like PPv2 does), mappers will eventually be able to find out which kind of maps are easier to play while maximising PP value. This opens up a trend in which new PP records are being broken because mappers get better at making PP maps, rather than because players are actually getting better. Just to be clear, players are getting better, but at least some (read: a substantial amount) of the reason players have been gaining more PP is because new PP maps are being created.
(Having over 8k PP was a lot more impressive with the maps that were available 3 years ago.)
But I don't really think it's fair to blame the mappers. If blame should go anywhere, it should go to the PP system itself, because that's probably the easiest thing to change in order to fix the problem.
One such exploit I can foresee in PP!Balance is that maps that require memorisation will be easier to gain PP on than other maps. Why is this?
In osu!, there are some maps can't be sightread well and require memorisation to score highly on (for example slider-heavy maps with varying slider velocity, because there is currently no way to read slider velocity before actually clicking the slider (should be fixed imo!)). These maps will have a lot of bad scores on them, and many of these scores will not be because the players lacked skill, but rather because they didn't bother to memorise how to play it.
Also, on PP!Balance, a play's PP value depends on the ratio between your score (using ScoreV2) and the average score.
Now imagine you try to sightread a memorisation map as described above. At first, your score will of course be bad because you couldn't read it. You're in the same position as many other players who played the map: their scores on the map are bad because they didn't bother to memorise it, so the average score on the map will be low. But for you, this is an opportunity! You can decide to memorise the map and therefore do much better than those who didn't. Let's say your original score was 0.1 of average, and your score after memorising the map is 10 times average.
The point is that it's much easier to go from 0.1 to 10 times the average by memorising rather than by getting better aim, speed, accuracy, finger control or other skills. The only way to go from 0.1 to 10 on a pure jump map that everyone can sightread perfectly is to get better at aim, and that's a lot harder than simply memorising a map.
To be honest, I don't think this exploit is as bad as the exploitability of the current PP system. Giving a disproportionate amount of PP for memorisation doesn't sound like too much of a problem, when everyone has the same ability to exploit it. But even so, there is a reason why this exploit may be less exploitable than you think.
And that reason is that on PP!Balance, every exploit of the system will become less exploitable the more it is exploited. For example, on that slider-heavy memorisation map I linked to above, if it turns out that it is easy to exploit it for PP simply by memorising it, more players will be motivated to memorise it. The more PP a map gives, the more players will be motivated to memorise it, causing the average score to go up. And the higher up the average goes, the less PP will be granted for high scores on it.
This leads to a really cool dynamic of players being forced to look for new maps to exploit as soon as the PP from the first map has been depleted. Instead of PP farmers we get PP hunter-gatherers, living a nomadic lifestyle always on their feet to find new lucrative caches of PP. This becomes a general force to equalise the PP territory, such that any map that is disproportionately easy to gain PP from will become proportionately easy to gain PP from.
And that's cool.
My original post sort of just mentioned the existence of differential popularity and said "let's hope it works anyway despite this glaring problem here!" I'm suitably embarrassed by this now, and I should have made a bigger effort to solve it before I posted this. Anyway, here's an update with what I think may be a solution to the problem. But first, I describe the problem in clearer terms so that my suggested solution will be easier to understand.
PP!Balance is an attempt at constructing a statistical method for measuring difficulty and skill (btw, Full Tablet has a really interesting example of a statistical measure in this thread). This is in contrast with direct methods of measuring difficulty and skill (PPv2 is an example).
The essential problem to creating a statistical measure is this. You have two sets of things, players and beatmaps. You want to measure the skill of the players, and the difficulty of the beatmaps. "Skill" is defined as the player's ability to score high on beatmaps, and "difficulty" is defined as the beatmap's ability to make the player score poorly on it. If we had a reliable measure of the difficulty of all beatmaps, then using that to determine the players' skill levels would be easy; and if we had a measure for the skill level of all players, using that to determine the difficulties of beatmaps would be easy. But since we start by knowing neither of the two, we have to find some trick to measure both at the same time.
One way of doing this would be to take a population of players with a constant average skill level, and then make them play all the beatmaps. The average scores that the population sets on each of the beatmaps would then be a pretty good measure of the difficulties of the beatmaps. If a population plays two different beatmaps, and the population's skill level remains constant, then a lower average score on one of the beatmaps means that that beatmap is harder (except for beatmaps where memorisation is important, as discussed earlier).
Unfortunately, no single population has played all the beatmaps. (Except maybe Toy and Blue Dragon.) So we're not guaranteed that the average scores on each of the beatmaps were set by the same average skill level. In fact, it's likely that the average scores on easier beatmaps were set by players with lower average skill level than the average scores on harder beatmaps. This is because players tend to seek out beatmaps with an appropriate difficulty level for them. We called this the "differential popularity problem".
So here's where my idea comes in.
Transitive Player Overlap Comparison
Definitions
M1, M2, M3 and so on are beatmaps.
P_M1 is the population of all players who have set a score on map M1.
P_M1 ∩ P_M2 is the population of all players who have set a score on map M1 AND map M2. We call this the "Alpha" population.
Algorithm
We first pick a map, M1, and then call the population that has set scores on that map the "Alpha population" so that it's easy to talk about. We define the difficulty of that map as the average score the Alpha population has set on it.
To determine the difficulties of other beatmaps, we estimate what the Alpha population would have scored on them if they had played those maps. But how will we estimate what the Alpha population would have scored on a beatmap, Mx, that Alpha hasn't actually played?
First, we find a beatmap, Mx, that has a population of at least 10,000 players (higher? lower?) who have set scores on Mx AND M1 within a timeframe of a week (higher? lower?) of each other. Actually, it doesn't have to be M1, it can just be any map we previously have an estimate for. Let's call that beatmap Ma, and the population that has played both Ma and Mx the "Beta population". In other words, we find a beatmap, Mx, for which the sentence "P_Ma ∩ P_Mx > 10,000" is true. (I discuss some details on this population search in the next section.)
Once we have found the Beta population, we compare the average scores that the Alpha and Beta populations have set on Ma.
If AlphaAvg(Ma)/BetaAvg(Ma) is greater than 1, then we know that the Alpha population is better than the Beta population. That means that we need to adjust BetaAvg(Mx) upwards in order to estimate AlphaAvg(Mx). In other words, we get the following formula.
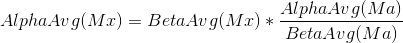
Repeat until we have an estimated AlphaAvg for all beatmaps, and then we use those averages when we measure the PP values of plays as described under the "Defining the range" section.
Also note that it's not necessary to estimate the AlphaAvg more than once per beatmap, so this becomes a static measure of difficulty. Thus PP values will not fluctuate as people set new scores on each beatmap, they'll stay the same.
Details on the population search
I mentioned in the introduction that I'm not sure exactly how this system will pan out if implemented and I don't have a way to check. If by magic coincidence, Cookiezi's FC on Image Material (honourable mention, La Valse also FCd it!) is worth less than any of my own scores ever, something has gone horribly wrong with the system and we need to figure out what before we actually implement it.
But after having tweaked the system to make it look about right for the scores currently in the database, I still think it's wise to have a public "testing period" to see how players react and if they can find bugs that no one thought of in the development period.
One way of doing this could be to show the PP!Balance value of plays and players on their profiles. This could be under the PPv2 values, inside parentheses and with a note that links to a post where they can get information and give feedback.
If the players dislike the system more than they like it, well, then that's a pretty good thing to know before it was implemented proper. No reason to make updates that make people net unhappy.
It's worth mentioning that people already seem to be pretty miffed with PPv2. The question is whether they'll be more miffed with this system. If you think about it... Most of the playerbase are not rank 1, so they are dissatisfied with their rank. Therefore, most of the playerbase will be happy about a change in the PP system, see it as an opportunity and think "maybe now I can become rank 1 faster?" Maybe?
What I see most people complain about with regards to the current PP system is how it fails to reward some skills (e.g. tech reading) and rewards other skills unfairly (e.g. aim). All these concerns can be summed up in one word: players want balance between skills. This here is a proposal that tries to do that automatically, with each skill rewarded proportional to the difficulty of attaining them.
I think this way of thinking about PP is the right way to go, but I can't guarantee that my preliminary version doesn't have flaws. My hope is just that if the osu!devs think it's worth the time, this system is tested on the database of scores that already exists, to see if it looks good and to check for weird cases. I can't do that myself because I don't have access to the database (except the top 100 plays on each map via the osu!api). Also, I don't want to pretend I have the definite solution to anything; Peppy and others will have much more experience thinking about this issue.
TL;DR: lol no, I'm not giving you a quick way out of this. Read the entire mind-bogglingly long thing. Also, there will be maths. :p
Background
This here is approximately the history of osu! PP systems.
Player A: Yo. I'm fantastic at aim. Can you give me some PP to recognise my achievements?
Peppy: Sure, let me change the algorithm to award PP based on aim.
Player B: Hey! I'm at least 10 times better at accuracy than that player is at aim, yet she has more PP than me. That's unfair!
Peppy: It's fine. Let me just tweak the algorithm to reward accuracy more.
-GN: *ahem* so what I can do is... well, it's kinda hard to explain. I'm better at what can only be called weird stuff than most other players, yet I don't get the amount of PP proportional to how difficult it is to be me. Here, have a look.
Peppy: what is that I don't even... ok, fine. I'll just tell the system to give you PP based on... how the heck do I tell the computer exactly what you're good at? Number of "wub"-sounds in a map? Complexity of sliders? Weight low-AR plays more? ...!? This seems at least NP-hard. Have a neat badge instead.
The complaints all seem to be some form of "the PP system does not weight X enough", where X can be skills like consistency, accuracy, sliders, tech reading, low-AR reading, etc.
And the proposed solutions to these complaints all seem to be some form of "weight skill X more". What I'm saying is that these kinds of solutions will never practically be sufficient, because we don't know exactly what kinds of skills being good at osu! requires, and we definitely don't know how to tell a computer what those skills are so that it can award PP based on them. So these types of solutions all seem to be a form of the typical error of applying specific solutions to a problem we can't specify.
The way to fix problems we can't specify is to offload the work of specifying the problem unto the solution itself. Yeah, uh, that was a confusing abstract garble of a sentence and I should start talking specifics.
The core idea
PP!Balance is a twofold system, just like PPv2. First, the PP value of a play is calculated, then the PP from that play is added to your total PP with the same weightage system that PPv2 uses.
Here's the weightage system explained from the wiki entry (you can skip this if you already know).
osu!wiki on the PP weighting System
Performance points use a weighted system, which means that your highest score ever will give 100% of its total pp, and every score you make after that will give gradually less.
This is explored in depth in the weightage system section of the article above. To explain this with a simpler example:
If your top pp rankings has only two maps played, all of which are 100pp each scores, your total pp would then be 195pp.
The first score is worth 100% of its total pp as it is your top score.
The second score is worth only 95% of its total pp as it is not your top score, so it contributes only 95pp towards your total instead of 100.
Now, let us posit that you set a brand new 110pp score. Your top rankings now look like this:
- 110pp, weighted 100% = 110
- 100pp, weighted 95% = 95
- 100pp, weighted 90% = 90
As you may have figured out, your new total pp is not simply 195 + 110 = 305pp, but instead 110 + 95 + 90 = 295pp.
This means that as you gradually improve at osu!, your pp totals will trend upwards, making your older scores worth progressively less compared to the newer, more difficult scores that you are updating them with.
The weightage system is necessary so that players can't gain more PP simply by setting more and more scores. If there were no weightage system in place, a player's PP would just be a measure of how many scores a player has set, not a measure of skill.
And how are the PP values for each play calculated?
The idea is that the PP of a play is supposed to measure how much better than others you are at that map. Call this the play's "Superiority". There are several ways to measure superiority of a play (e.g. rank achieved on map, percent score of top score, difference between the score and avg score and so on), and I talk about which way I think works best in the next section.
The essential difference between PP!Balance and PPv2 is that, unlike PPv2, PP!Balance doesn't try to directly define what it is exactly that is difficult in a beatmap (e.g. aim, accuracy, speed, reading, finger control, stamina and so on). Instead it lets the difficulty of a map be determined empirically by players' ability to play it.
If the hardest beatmap in the game is actually a lot more difficult than its low 5* rating suggests, you should get more PP for FCing it than for other maps of the same star rating. In fact, the ezpp! plugin tells me that you get 179pp and 201pp for SSing each of the maps respectively on the current PP system, so it does even worse worse than equal.
The PP system I'm proposing would give much more PP for FCing Scarlet Rose than the Veela map because FCing Scarlet Rose is very much better than most other players can do on the map. FCing the other map is still better than most, but it isn't as much better than an FC on Scarlet Rose is, so you won't get as much PP for it.
This also means that you can gain PP by being good at whatever you want, as long as there are ranked beatmaps for it. If you're not much better than others at aim, but you're still much better than others at tech reading, then you'll have an easier time gaining PP by playing tech maps than aim maps.
The players with the highest PP on this ranking system would then tend to be the players who are most better than others, which sounds sort of correct. In PPv2, the highest ranked players tend to be those who are best at a combination of aim, speed and accuracy, mostly ignoring other skills required to do well on beatmaps in osu!.
Here be maths
I will now proceed to cobble together the formula I think works best for calculating PP. I'm not sure this is the best formula possible. But instead of giving you my best suggestion first, I'm going to take you through some steps I personally went through in order to arrive at my best suggestion. I want to show you that there are options here, and I need to discuss them in order to explain why I think my latest version works best.
If you don't understand the technical details, you can still understand the system in broad strokes from the previous section and then give constructive feedback on it. No feedback is stupid (but pls don't yell at me).
So without further ado,
First idea: Rank-based superiority
My first thought was just, why not use the play's rank on the beatmap? If you get first place you get more PP than if you get 2nd place, and so on. We note that the difference in difficulty between the 1st and 2nd rank usually tends to be much greater than the difference in difficulty between the 101st and 102nd rank, so we conclude that there is something like a logarithmic distribution in the difficulty of attaining map ranks. Therefore the PP value of the scores should also scale logarithmically. We end up with something like this. (edit: Was PPv1 something similar? osu!wiki doesn't say.)
In the first term, N is the number of other plays made on that map (including your own plays and failed plays) set within 365 days past. The more plays-within-a-year a beatmap has, the more PP you get for getting a high score on it. The time limit is necessary to not unfairly disadvantage new maps that are just as hard as old maps but have fewer plays on them.
The reason why the PP of a play should depend on N is that the more people try a beatmap, the higher the competition is for getting high ranks on it. It is more difficult to win competitions where lots of other players compete, so you deserve more PP for ranking highly on them.
k is a constant weight that determines the importance of N. For example, say that k = 10,000. Then if you set a score on a beatmap with a 200,000 within-year play count, you multiply the play's PP value by 20. Or if the within-year play count was only 5,000, then you multiply the play's PP value by 0.5. It could also be that a different scaling of N works better.
The second term (1/ln(stuff)) is supposed to scale inversely logarithmically with your rank on a beatmap. Calculating for a few values of MapRank, we see that the PP value of 1st place gets multiplied by 1, 2nd place by 0.76, 101st by 0.2159, 102nd by 0.2154, and so on. It checks out.
(e-1 is there in the logarithm to make sure that the term equals 1 for MapRank = 1. If I instead wrote 1/ln(MapRank) without the e-1, then the term would equal 1/ln(1) when MapRank = 1. And since ln(1) = 0, you would have to divide by zero, and that is bad.)
The reason why I think this way of calculating PP is a bad idea is because on some maps, you see many players share the same score at the top, and it would be unfair to give different amounts of PP to players for exactly the same performance. And the corollary is that on other maps, the first ranks are arguably a lot better than any of the other scores, and this system isn't sensitive to degrees of superiority like that.
Second idea: ScoreV1-based superiority
Take your score and divide it by the average score on that beatmap. If your score is exactly average, then PP_play = 1. If your score is 100 times greater than average, PP_play = 100. If your score is exactly half the average score, PP_play = 0.5. This system can then tell the difference between a score which is barely 1st place and a score which is way above what's needed for 1st place, and give PP accordingly. The idea assumes that average score on a beatmap is a good proxy for how difficult it is.
We can easily do some magic to make PP values range from 1 if the score is 100 times lower than average and 1000 if the score is 100 times greater than average. But the core idea is easier to represent with the simple equation above. We'll make the PP values have sensible ranges later.
It's probably wisest to take the average of all the top scores set by all players who have played the map (so if you play the map twice, only the top score gets counted when calculating the average). This is to prevent people from being able to purposefully set lots of bad scores on a map in order to drag down the average, making their top play worth more PP.
The main reason I think this system is insufficient is because it inherits the purposes and flaws of the current scoring system. A lot of players complain that accuracy has little effect on score, and indeed that would mean that accuracy has little effect on PP values in this system.
We have a few options here. The first option is to record all plays players make on maps, calculate what their ScoreV2 scores would be (even if they played using ScoreV1, we just recalculate using ScoreV2), and then do the PP!Balance calculations using those scores. Or we can invent a new scoring system and do the same with that. I prefer using ScoreV2, but you're free to argue why using something else is better.
Third idea: ScoreV2-based superiority
If a beatmap uses ScoreV1 for its leaderboards, then your top score on that leaderboard may not necessarily be the top PP play, because ScoreV1 and ScoreV2 is calculated differently. This is actually a problem with the current PP system, where you can make plays with a higher score but lower PP value, causing you to lose PP. If beatmap leaderboards will continue to stay ScoreV1, then I think the solution to this is just to keep two leaderboards for each beatmap, one for each scoring method, and then just make the ScoreV2 leaderboard hidden. That way, you can make plays that have a higher ScoreV1 value than ScoreV2 value without losing PP.
For the purposes of the PP calculations, the average score on the beatmap would then be the average of the hidden ScoreV2 leaderboard. If a player has played the beatmap twice, only their top ScoreV2 play gets counted into the average.
A problem with this way of doing it is that different maps have different HP values. For example, Airman has an HP of 3. This means that it will have a lot more bad scores than if the HP value was 7, dragging the average down considerably compared to maps with an HP value of 7. And since the average goes down, all the plays' PP values go up, making it easier to gain PP from maps with low HP value. And that's bad, because maps with lower HP values aren't necessarily harder than maps with higher HP values.
The solution seems to have to be some way of dealing with failed scores: the more failed scores a beatmap has, the more PP should be given. One way of dealing with this could be to just submit failed scores (i.e. their ScoreV2 values up until the point they failed) into a hidden database for that beatmap, and then include those scores when calculating the average score on that beatmap.
But this gives too much of an advantage to maps with high HP values. For example, I bet I'm not the only noob who has tried to play DoKito's Yomi Yori (HP = 6) several times only to fail horribly at the first stream. A large number of those plays would have gotten a much higher score if they were played on an identical beatmap with HP 4. Thus the HP 6 version would have had a lower average score if we add the failed scores.
So I think we need a more creative solution to the HP bar problem. EDIT 11/02/2018: The solution to this problem is really easy. (Thanks to Omnipotence -.) Just calculate the average score on a beatmap from the subset of the scores that would have passed if the beatmap had an HP value of 10. This way, the PP system treats all maps as if they had HP 10, so the actual HP value of a map won't affect the PP possible to gain from the map.
Another issue with this third idea is that some maps are popular for almost exclusively very new players, and other maps are popular for almost exclusively very good players. It will therefore be easier to do better than others on the former type of maps than on the latter type of maps.
Let's call this problem "differential popularity" (better players tend to play harder maps, less good players tend to play easier maps) so that it's easier to talk about. This is actually also a problem in the first and second ideas, and it makes it hard to reliably measure the real difficulty of beatmaps. (Edit: I wrote a section on solving this problem later in this post.)
Having explained why I think this is the way we should define PP values, we now turn to finding a way to make this formula have the proper range of values.
Defining the range
I think the difference in PP values of the worst play to the current best play should be something like a 1000 PP. A bit less or a bit more is fine. This is approximately the range of the current PP system. Maybe the new system should have slightly higher values because then the transition won't make many players angry about "losing" PP?
Anyway, here's the formula I think has the best scaling. I won't go into how I arrived at this equation, but if you need to know you can ask me.
Where we define the S variable ("Superiority") with the formula from the previous section.
In other words, S is the ratio of the ScoreV2 value of your play and the average ScoreV2 values of all the plays on the dedicated ScoreV2 leaderboard (see the first paragraph in the previous section).
PPfloor is the lowest value of S we want to give PP to. We give 0 PP to all scores below it. I think plays that have an S value of less than 0.01 can safely be given 0 PP to, because I think even the newest players can find maps they can achieve an S of above 0.01 on (but if I'm wrong, we can set PPfloor even lower). Consider, in order to achieve an S of lower than 0.01, you must score (ScoreV2) something like 5,000 on maps that have an average score of 500,000. So PPfloor = 0.01 looks good to me.
k_1 and k_2 are constants that determine the range of PP values. If we set k_1 = 2.5 and k_2 = 100 then the range for different values of S looks like this.
To achieve 1256 PP, you need to score a thousand times better than average. For example by scoring 1,000,000 (nomod SS) on a map with average score of 1,000. You can fiddle with the constants in this Google spreadsheet to see what they do (anyone with link can edit).
I'm not sure what the best weighting is. I think the way to find out is to set the weights to something and then use the formula to calculate a bunch of PP values from plays that have already been set, and see if it the results look about right.
Also, I think it'd make sense to not give plays on a map PP before at least a thousand players have set scores on the map. Otherwise the PP values of the plays would be too dependent on random initial conditions.
Formula explained with an example
Imagine I set the number one score on xi - FREEDOM DiVE [FOUR DIMENSIONS] (normal score for me tbh). A HDHR SS worth 1,120,000 points on ScoreV2. Let's also say that the average ScoreV2 on that beatmap is 100,000 (I have no idea). So that gives us an S of 11.2. Assume we use the same weighting of the constants as I gave them in the section on "Defining the range".
The amount of PP I would get would then be...
Exploitability: PP farmers vs. PP hunter-gatherers
In any PP system that tries to directly define what "difficulty" is (e.g. by defining it as a function of aim, speed, accuracy and strain like PPv2 does), mappers will eventually be able to find out which kind of maps are easier to play while maximising PP value. This opens up a trend in which new PP records are being broken because mappers get better at making PP maps, rather than because players are actually getting better. Just to be clear, players are getting better, but at least some (read: a substantial amount) of the reason players have been gaining more PP is because new PP maps are being created.
(Having over 8k PP was a lot more impressive with the maps that were available 3 years ago.)
But I don't really think it's fair to blame the mappers. If blame should go anywhere, it should go to the PP system itself, because that's probably the easiest thing to change in order to fix the problem.
One such exploit I can foresee in PP!Balance is that maps that require memorisation will be easier to gain PP on than other maps. Why is this?
In osu!, there are some maps can't be sightread well and require memorisation to score highly on (for example slider-heavy maps with varying slider velocity, because there is currently no way to read slider velocity before actually clicking the slider (should be fixed imo!)). These maps will have a lot of bad scores on them, and many of these scores will not be because the players lacked skill, but rather because they didn't bother to memorise how to play it.
Also, on PP!Balance, a play's PP value depends on the ratio between your score (using ScoreV2) and the average score.
Now imagine you try to sightread a memorisation map as described above. At first, your score will of course be bad because you couldn't read it. You're in the same position as many other players who played the map: their scores on the map are bad because they didn't bother to memorise it, so the average score on the map will be low. But for you, this is an opportunity! You can decide to memorise the map and therefore do much better than those who didn't. Let's say your original score was 0.1 of average, and your score after memorising the map is 10 times average.
The point is that it's much easier to go from 0.1 to 10 times the average by memorising rather than by getting better aim, speed, accuracy, finger control or other skills. The only way to go from 0.1 to 10 on a pure jump map that everyone can sightread perfectly is to get better at aim, and that's a lot harder than simply memorising a map.
To be honest, I don't think this exploit is as bad as the exploitability of the current PP system. Giving a disproportionate amount of PP for memorisation doesn't sound like too much of a problem, when everyone has the same ability to exploit it. But even so, there is a reason why this exploit may be less exploitable than you think.
And that reason is that on PP!Balance, every exploit of the system will become less exploitable the more it is exploited. For example, on that slider-heavy memorisation map I linked to above, if it turns out that it is easy to exploit it for PP simply by memorising it, more players will be motivated to memorise it. The more PP a map gives, the more players will be motivated to memorise it, causing the average score to go up. And the higher up the average goes, the less PP will be granted for high scores on it.
This leads to a really cool dynamic of players being forced to look for new maps to exploit as soon as the PP from the first map has been depleted. Instead of PP farmers we get PP hunter-gatherers, living a nomadic lifestyle always on their feet to find new lucrative caches of PP. This becomes a general force to equalise the PP territory, such that any map that is disproportionately easy to gain PP from will become proportionately easy to gain PP from.
And that's cool.
Edit: Solving the differential popularity problem
My original post sort of just mentioned the existence of differential popularity and said "let's hope it works anyway despite this glaring problem here!" I'm suitably embarrassed by this now, and I should have made a bigger effort to solve it before I posted this. Anyway, here's an update with what I think may be a solution to the problem. But first, I describe the problem in clearer terms so that my suggested solution will be easier to understand.
PP!Balance is an attempt at constructing a statistical method for measuring difficulty and skill (btw, Full Tablet has a really interesting example of a statistical measure in this thread). This is in contrast with direct methods of measuring difficulty and skill (PPv2 is an example).
The essential problem to creating a statistical measure is this. You have two sets of things, players and beatmaps. You want to measure the skill of the players, and the difficulty of the beatmaps. "Skill" is defined as the player's ability to score high on beatmaps, and "difficulty" is defined as the beatmap's ability to make the player score poorly on it. If we had a reliable measure of the difficulty of all beatmaps, then using that to determine the players' skill levels would be easy; and if we had a measure for the skill level of all players, using that to determine the difficulties of beatmaps would be easy. But since we start by knowing neither of the two, we have to find some trick to measure both at the same time.
One way of doing this would be to take a population of players with a constant average skill level, and then make them play all the beatmaps. The average scores that the population sets on each of the beatmaps would then be a pretty good measure of the difficulties of the beatmaps. If a population plays two different beatmaps, and the population's skill level remains constant, then a lower average score on one of the beatmaps means that that beatmap is harder (except for beatmaps where memorisation is important, as discussed earlier).
Unfortunately, no single population has played all the beatmaps. (Except maybe Toy and Blue Dragon.) So we're not guaranteed that the average scores on each of the beatmaps were set by the same average skill level. In fact, it's likely that the average scores on easier beatmaps were set by players with lower average skill level than the average scores on harder beatmaps. This is because players tend to seek out beatmaps with an appropriate difficulty level for them. We called this the "differential popularity problem".
So here's where my idea comes in.
Transitive Player Overlap Comparison
Definitions
M1, M2, M3 and so on are beatmaps.
P_M1 is the population of all players who have set a score on map M1.
P_M1 ∩ P_M2 is the population of all players who have set a score on map M1 AND map M2. We call this the "Alpha" population.
Algorithm
We first pick a map, M1, and then call the population that has set scores on that map the "Alpha population" so that it's easy to talk about. We define the difficulty of that map as the average score the Alpha population has set on it.
To determine the difficulties of other beatmaps, we estimate what the Alpha population would have scored on them if they had played those maps. But how will we estimate what the Alpha population would have scored on a beatmap, Mx, that Alpha hasn't actually played?
First, we find a beatmap, Mx, that has a population of at least 10,000 players (higher? lower?) who have set scores on Mx AND M1 within a timeframe of a week (higher? lower?) of each other. Actually, it doesn't have to be M1, it can just be any map we previously have an estimate for. Let's call that beatmap Ma, and the population that has played both Ma and Mx the "Beta population". In other words, we find a beatmap, Mx, for which the sentence "P_Ma ∩ P_Mx > 10,000" is true. (I discuss some details on this population search in the next section.)
Once we have found the Beta population, we compare the average scores that the Alpha and Beta populations have set on Ma.
If AlphaAvg(Ma)/BetaAvg(Ma) is greater than 1, then we know that the Alpha population is better than the Beta population. That means that we need to adjust BetaAvg(Mx) upwards in order to estimate AlphaAvg(Mx). In other words, we get the following formula.
Repeat until we have an estimated AlphaAvg for all beatmaps, and then we use those averages when we measure the PP values of plays as described under the "Defining the range" section.
Also note that it's not necessary to estimate the AlphaAvg more than once per beatmap, so this becomes a static measure of difficulty. Thus PP values will not fluctuate as people set new scores on each beatmap, they'll stay the same.
Details on the population search
- The limited timeframe is there to ensure that the population's average skill level is the same when they're playing the first beatmap as when they're playing the second beatmap. For example, say we want to measure the relative difficulty of a 3* beatmap and a 6* beatmap. If we didn't specify a timeframe, it could be that the same population played the 3* beatmap an average of 1 year earlier than they played the 6* beatmap. We can expect players to get better over time, so their average skill would be higher when they played the 6* beatmap than when they played the 3* beatmap, and our attempt to measure the relative difficulty would fail.
- We can also require that the all the players in the population has played both beatmaps at least 10 times each (or more). This will lessen score differences due to the memorisation problem (discussed earlier), because the players have had time to memorise both maps. Further score differences will then be due to differences in how much of other skills (aim, speed, sliders, reading, etc.) the maps require, and not due to memorisation.
- This system will work badly for maps that are popular with very new players. Because even if we limit the population search to players who have played both beatmaps within a day of each other, very new players can improve substantially within a day, so the population's average skill level may be different while playing the two maps. To prevent this, we can limit the population search to players who have a playtime of at least 100 hours or something. Players who have played a lot already see less improvement per hour than very new players.
- Instead of searching for the first beatmap with the criteria listed above, the population search could rather search for a beatmap with the highest combined measure of 1) largest common population between the two beatmaps, 2) shortest timeframe between players playing the two beatmaps, 3) highest player playtime, and 4) highest number of times that each player has played both beatmaps.
Testing period before full transition
I mentioned in the introduction that I'm not sure exactly how this system will pan out if implemented and I don't have a way to check. If by magic coincidence, Cookiezi's FC on Image Material (honourable mention, La Valse also FCd it!) is worth less than any of my own scores ever, something has gone horribly wrong with the system and we need to figure out what before we actually implement it.
But after having tweaked the system to make it look about right for the scores currently in the database, I still think it's wise to have a public "testing period" to see how players react and if they can find bugs that no one thought of in the development period.
One way of doing this could be to show the PP!Balance value of plays and players on their profiles. This could be under the PPv2 values, inside parentheses and with a note that links to a post where they can get information and give feedback.
If the players dislike the system more than they like it, well, then that's a pretty good thing to know before it was implemented proper. No reason to make updates that make people net unhappy.
It's worth mentioning that people already seem to be pretty miffed with PPv2. The question is whether they'll be more miffed with this system. If you think about it... Most of the playerbase are not rank 1, so they are dissatisfied with their rank. Therefore, most of the playerbase will be happy about a change in the PP system, see it as an opportunity and think "maybe now I can become rank 1 faster?" Maybe?
Questions and Answers
But Mio, this will completely ruin the current PP farming mapping meta!
This is a FEATURE. Not bug. Definitely not a bug.
What about FL, HT and EZ? Won't they be overvalued?
My first response is you can't even EZHTFL and you call yourself an osu!player? My second response is, actually, these mods may be overvalued on this system if they are overvalued on ScoreV2. I'm not an expert on any of these mods, so I don't have a good feel for how difficult they are compared to nomod.
If all the top PP plays in this system turn out to be EZ, HT and/or FL scores, that probably means that the system is imbalanced. Most plays are not EZ, HT or FL, so that makes it suspicious that the most difficult play will be with one of these mods.
A potential PP treasure throve for EZ players are maps like Yomi Yori. The average ScoreV2 of that map will be pretty low since it's such a difficult map, so getting a good score on it will be worth a lot of PP. But getting a good score on it will be easier with EZ or HT, so is their PP value balanced?
I don't know. Is idke's FC on HT more impressive than firebat92's nomod score (currently one rank below)? I suspect more good players have played that map on nomod than on HT, yet we find more HT scores in the top 50 than nomod scores. This is probably because using HT makes it less difficult to set high scores than on nomod. Same reasoning for EZ. I'm assuming that the leaderboards look similar on ScoreV2. Time Freeze is another good example.
(Also, yes, I do realise that EZ and HT makes maps much harder to read, so they are really impressive in their own way. But I stress that I'm really not an expert on any of this, so if I say stuff that is inexcusably wrong, please correct me.)
I don't know if FL is balanced either. rrtyui's FL score on Neuronecia is worth approximately as much as other HDHR scores on it. Should the FL score be worth more or less? This all warrants more testing than I can do.
A possible solution to this is to calculate the PP for EZ, HT and/or FL scores against an average score that only counts scores made with the same mods. But because most maps will not have at least a thousand players who have played with these mods on, EZ/HT/FL players will not be able to gain PP from most maps. This seems bad, so I wouldn't advocate this as a solution unless testing seems to indicate that they are overvalued.
(While we're on the topic of balancing mods: The score modifier for HD ought obviously to scale inversely with AR.)
If all the top PP plays in this system turn out to be EZ, HT and/or FL scores, that probably means that the system is imbalanced. Most plays are not EZ, HT or FL, so that makes it suspicious that the most difficult play will be with one of these mods.
A potential PP treasure throve for EZ players are maps like Yomi Yori. The average ScoreV2 of that map will be pretty low since it's such a difficult map, so getting a good score on it will be worth a lot of PP. But getting a good score on it will be easier with EZ or HT, so is their PP value balanced?
I don't know. Is idke's FC on HT more impressive than firebat92's nomod score (currently one rank below)? I suspect more good players have played that map on nomod than on HT, yet we find more HT scores in the top 50 than nomod scores. This is probably because using HT makes it less difficult to set high scores than on nomod. Same reasoning for EZ. I'm assuming that the leaderboards look similar on ScoreV2. Time Freeze is another good example.
(Also, yes, I do realise that EZ and HT makes maps much harder to read, so they are really impressive in their own way. But I stress that I'm really not an expert on any of this, so if I say stuff that is inexcusably wrong, please correct me.)
I don't know if FL is balanced either. rrtyui's FL score on Neuronecia is worth approximately as much as other HDHR scores on it. Should the FL score be worth more or less? This all warrants more testing than I can do.
A possible solution to this is to calculate the PP for EZ, HT and/or FL scores against an average score that only counts scores made with the same mods. But because most maps will not have at least a thousand players who have played with these mods on, EZ/HT/FL players will not be able to gain PP from most maps. This seems bad, so I wouldn't advocate this as a solution unless testing seems to indicate that they are overvalued.
(While we're on the topic of balancing mods: The score modifier for HD ought obviously to scale inversely with AR.)
You need to balance the amount of balance in your PP!Balance, otherwise we'll have too much balance!
I can imagine the complaint,
Hypothetical Player: "Look, I actually just want the PP system to balance the skills I like. No silly stuff! Can you even imagine what crazy people like Ekoro, Riviclia, Mafham and their gang will become good at next?"
With exception to the EZ, FL and HT mods (discussed in the previous section), I don't think this will be a problem. The beauty of this system is that when mappers create new creative maps that are difficult in some hitertho unknown way, then players can try to gain PP by becoming better at those kinds of maps.
"Yeah, he's just good at s-such weird maps."
(OWC commentator on -GN carrying his team on Graces of Heaven)
Hypothetical Player: "Look, I actually just want the PP system to balance the skills I like. No silly stuff! Can you even imagine what crazy people like Ekoro, Riviclia, Mafham and their gang will become good at next?"
With exception to the EZ, FL and HT mods (discussed in the previous section), I don't think this will be a problem. The beauty of this system is that when mappers create new creative maps that are difficult in some hitertho unknown way, then players can try to gain PP by becoming better at those kinds of maps.
(OWC commentator on -GN carrying his team on Graces of Heaven)
This system fails to balance accuracy
The argument goes: in (the current version of) ScoreV2, 30 % of your score is determined by accuracy. Some players may think this is too little, other players may think this is too much. Since PP!Balance uses ScoreV2 for its calculations, the complaints about accuracy in ScoreV2 also apply to PP!Balance.
I think this is true, but only partially. Players who are best at accuracy will still be able to get a lot of PP by playing maps where the average score is lower because they are maps that are especially hard to acc. If your strength is accuracy, you'll have an easier time doing better than others on these maps, thus those maps (instead of, say, aim maps) will be "farm maps" for you. (I'm sorry, I'm not sure which maps those actually are so I can't give any examples.)
I think this is true, but only partially. Players who are best at accuracy will still be able to get a lot of PP by playing maps where the average score is lower because they are maps that are especially hard to acc. If your strength is accuracy, you'll have an easier time doing better than others on these maps, thus those maps (instead of, say, aim maps) will be "farm maps" for you. (I'm sorry, I'm not sure which maps those actually are so I can't give any examples.)
ScoreV2 isn't sensitive to the length of beatmaps, so this system overvalues short maps
Not really. It is true that short maps gives more room for luck to determine the outcome of the score,
but this is true for all players equally. So it doesn't make it easier to be better than others at the map, which is what determines the PP value.
but this is true for all players equally. So it doesn't make it easier to be better than others at the map, which is what determines the PP value.
How do you upload math equations as images quickly?
Write the maths in LaTeX using this website, then download that as a png, and then drag that png to the ShareX (I can't use puush because they aren't accepting new users at the moment) window so that it uploads it and gives you an url.
(Why forum not already have LaTeX support?!)
(Why forum not already have LaTeX support?!)

 If acc and speed were buffed I still wouldn't like my top ranks so the only thing I'm whining about for myself is separating skills into different pp categories
If acc and speed were buffed I still wouldn't like my top ranks so the only thing I'm whining about for myself is separating skills into different pp categories