wat de pak :v ngapain direply,harusnya lu reply kalau ada user dari negara lain :vEnder Lain wrote:
kalo ini mah nggak perlu pake google translate kali ya?
forum
Use google translate to say something in the user above's country language.
posted
Total Posts
105
Saya bertanya-tanya mengapa ada begitu banyak orang dari asia tenggara bermain osu !.
Voici une blague très amusante à propos des Canadiens ayant des conneries de langues nationales. Putain le linguistes.
og
Here is a very funny joke aboiut Canadians having fuckton of national languages. Fucking le linguists.
что-то
Oh dios mio ¡CÓMO PARA MÍ, ES INTERESANTE! PETROSYAN DEL AÑO!
wut. have you ever read the thread title?DatMan212 wrote:
CKYA BLYAT
OT: Oh my God! He yells "BIT FUCK." What an intellectual he is!
"Oh god! He's yelling "CYKA BLYAT". What an intellectual!"
Olet minun violetti
我希望这是正确的语言,我知道中国是语言最多的国家之一。 无论如何,让我写一些更多的文字,当你阅读它时,它会为你翻译更有趣的内容,你不同意吗?
J'aime le sirop d'érable et le froid. Aussi le Canada n'est pas un vrai pays
Ohh, agudo! Ají Sin embargo, nunca lo he intentado. Y realmente no me gusta la comida picante.
Saya agak sedih bahwa utas ini mati sehingga saya akan menghidupkannya kembali dengan pos ini. Sangat gila bagaimana utas dapat mengambil traksi dengan sangat cepat dan mati dengan cepat.
salut tout le monde. Je suis un weeaboo russe qui a cessé de regarder des dessins animés au profit de romans japonais.
translated from nihongo:
Мир - лучший в мире стенд
for the sake of thread relevancy let's pretend that english speakers speak other languages kthx
Мир - лучший в мире стенд
for the sake of thread relevancy let's pretend that english speakers speak other languages kthx
And the sense of pretending? You can just translate from your native language well, or translate twice.
OG: А толку прикидываться? Можно же просто перевести с родного языка ну или перевести два раза.
Proper TL: What's the point of pretending? Can't you just translate it from your native language or transtale back and forth?
OG: А толку прикидываться? Можно же просто перевести с родного языка ну или перевести два раза.
Proper TL: What's the point of pretending? Can't you just translate it from your native language or transtale back and forth?
Мне любопытно о разнице между переводом с оригинального языка переводом с английского.
emm...emang yang ini masih perlu pake google terjemahan ya? :v
DeletedUser_13780435
i agree!
SPOILER!
Well I dunno. Some shit about burgers, obesity and growing Trump's wigs on the farmland.
What other American setereotypes are there?
Oh yeah, those fuckign commies!
I guarantee that it will translate into some garbled mess.
What other American setereotypes are there?
Oh yeah, those fuckign commies!
I guarantee that it will translate into some garbled mess.
i hate my old posts
I will be ignoring the post above this, and instead do it on myself, for obvious reasons. (low effort, bad joke)

Я думаю, я должен передать это тебе. Вы действительно использовали мою команду. Молодцы, наверное. Но не забывайте: они собираются исправить эту утечку газа в какой-то момент, и когда они это сделают ... КОГДА ОНИ ДЕЛАЮТ ... это возвращается к делу, приятель. НЕТ БОЛЬШЕ, МИССИС, Ницца, я. Продолжать.
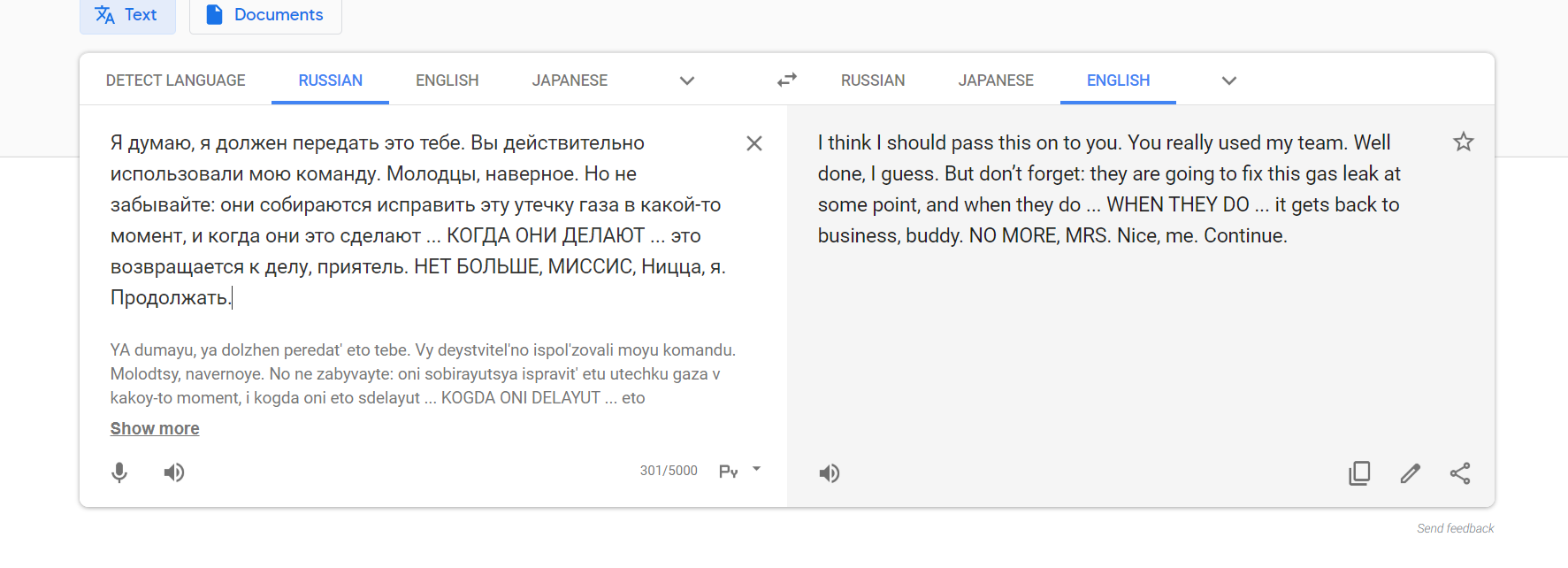
original text lmao
I guess I gotta hand it to ya. You really hosed my crew. Well done, I guess. But jus’ remember: they’re gonna fix this gas leak at some point and when they do… WHEN THEY DO… it’s back to business, buddy. NO MORE MRS NICE ME. Carry on.
Wala akong ideya kung ano ang sasabihin, sa palagay ko ay dapat sabihin ang isang bagay na maganda.
Kumusta! Ikaw ay isang kamangha-manghang tao.
Kumusta! Ikaw ay isang kamangha-manghang tao.
Мы ESL должны были сделать это, потому что говорить по-американски напрямую хромает
Yandex Translate is a better service if you want to translate Russian
мне нравится русский язык
sinusta, jos pidät siitä
Saya harap Anda memiliki hari yang menyenangkan
Luonto on poikkeuksellinen, huolimatta ihmisen keksimästä vaikuttavasta tekniikasta vuosien varrella, se hallitsee edelleen kaikkia levyjä. Luonnon on voitettu helposti korkeimman lämpötilan ennätys. Meidän ei tarvitse etsiä kovasti löytääksesi paljon korkeampaa lämmönlähdettä kuin mitä ihminen on onnistunut tuottamaan, meillä on vain 'katsomaan aurinkoamme, joka lämmittää meitä huolimatta siitä etäisyydestä, joka erottaa meidät. Joten päätimme mitata kokeellisesti auringon lämpötilaa.
Tätä varten käytämme mustaksi maalattua alumiinilevyä, joka on sijoitettu kehykseen eristääksesi sen termisesti vain yhdellä paljaalla puolella. Annamme sen lämpötilan laskea tasapainoon ympäristön kanssa. Sitten sijoitamme sen niin, että sen pinta on kohtisuorassa auringon säteen kanssa ja merkitsemme sen lämpötila 30 sekunnin välein 5 minuutin ajan.
Mitattujen arvojen avulla teemme graafin lämpötilasta ajan funktiona. Yhtälön Q = mc * ΔT avulla havaitun kaltevuuden tulisi olla suora, kunhan alumiinilevyn ja ympäristön välillä ei ole lämmönvaihtoa. Koska on mahdotonta estää lämmönvaihtoa ympäristön ja alumiinilevyn välillä, havaitsemme hetkeä, jolloin kuvaajan kaltevuus lakkaa olemasta suoraviivainen ja leikkaa kaikki arvot yli tämä kohta pitää vain kohdat, joissa alumiinilevyn ja ympäristön välillä oli vähän lämmönvaihtoa.
Käytämme sitten yhtälöä W = (mc * ΔT) / t1 levylle vastaanotetun aurinkovoiman laskemiseksi. Jos jaamme aurinkoenergian, joka vastaanotetaan tämän voiman saaneen alumiinilevyn pintaan, saadaan yhtälön I = W / m ^ 2 mukaan auringon vastaanottama aurinkovoimakkuus.
Mittaa sitten maa-aurinkoetäisyyden ja auringon säteen (Rs / r) välinen suhde. Tätä varten projisoimme aurinkokuvan ruudulla ympyräpiirustuksella. Projisoimme kuvan niin, että se on täydellisesti ympyrän keskellä, ja sitten laskemme sekuntien lukumäärän ennen kuin aurinkokuva on kokonaan ympyrän ulkopuolella. Tietäen, että maapallosta nähty aurinko kulkee 360 astetta ympäri maata 24 tunnissa, laskemme kuinka paljon aurinko kulkee t sekunnissa.
Kaavion mukaan tan 〖(θ / 2) = (Rs / r)〗 pystymme laskemaan (Rs / r) käyttämällä tätä yhtälöä.
Yhtälöllä I = σ * (Rs / r) ^ 2 * 〖T_s〗 ^ 4, missä σ edustaa Stefan-Boltzmann-vakioita, R_s / r edustaa maapallon-aurinkoetäisyyden ja auringon säteen välistä suhdetta ja T_s edustaa auringon lämpötilaa, pystymme laskemaan auringon lämpötilan aiemmin laskettujen arvojen perusteella kirjoittamalla yhtälön arvoksi T_s = ∜ (I / (σ * 〖tan (θ / 2)〗 ^ 2)) .
On muistettava, että menetelmämme ei ota huomioon maan ilmakehän, joka estää 30–40% auringonsäteistä leveysasteellamme. Tämä tarkoittaa, että löytämämme arvojen tulisi olla alhaisemmat kuin auringon lämpötilan teoreettinen arvo. Joten teemme kaksi laskelmaa, laskelman, jossa ei oteta huomioon ilmakehää, ja laskelman, joka otetaan huomioon jakamalla kokeellisen intensiteetin arvo sädekappaleen prosenttimäärällä teoreettisella ilmakehällä, joka on 35 %.
keskustelu
Kokeelle 1 saadut arvot ovat 4993 ° K oikaistamattomana arvona ja 6492 ° K oikaistuna arvona. Jos verrataan näitä kahta arvoa teoreettisesti hyväksytyyn teoreettiseen arvoon 5778 ° K, saadaan prosentuaaliset erot -13,6% oikaistamattomalle ja 12,3% oikaistulle arvolle. Nämä arvot eivät ole kovin kaukana teoreettisesta arvosta käytetyn alkeellisen menetelmän kannalta. En kuitenkaan usko, että tämä essee tuottaa hyviä tuloksia. Menetelmämme virheiden syiden, joista keskustellaan myöhemmin tässä keskustelussa, pitäisi johtaa meidät teoreettista arvoa alempiin arvoihin. Koe-auringon lämpötila-arvo on kuitenkin säädetty ja korkeampi kuin teoreettinen arvo. Todennäköisin syy on, että levy ei ollut lämpötilatasapainossa ympäristön kanssa kokeen alussa, joten lämpötilaero olisi suurempi ja antaisi siten korkeamman auringon lämpötila-arvon kuin ennakoida. Tätä voidaan tukea sillä, että testin 1 aika-lämpötila-kuvaajassa arvojen lineaarisuus katkeaa hyvin varhaisessa vaiheessa kuvaaen, että levy on alkanut vaihtaa lämpöä ympäristössä. Tämä lineaarisuuskatko syntyy paljon aikaisemmin kuin vastaavassa kuvaajassa testille 2, jossa arvot pysyivät lineaarisina koko kuvaajan suhteen, mikä osoittaa, että levy ei ollut vielä alkanut tehdä lämpötilanvaihtoa.
Tätä varten käytämme mustaksi maalattua alumiinilevyä, joka on sijoitettu kehykseen eristääksesi sen termisesti vain yhdellä paljaalla puolella. Annamme sen lämpötilan laskea tasapainoon ympäristön kanssa. Sitten sijoitamme sen niin, että sen pinta on kohtisuorassa auringon säteen kanssa ja merkitsemme sen lämpötila 30 sekunnin välein 5 minuutin ajan.
Mitattujen arvojen avulla teemme graafin lämpötilasta ajan funktiona. Yhtälön Q = mc * ΔT avulla havaitun kaltevuuden tulisi olla suora, kunhan alumiinilevyn ja ympäristön välillä ei ole lämmönvaihtoa. Koska on mahdotonta estää lämmönvaihtoa ympäristön ja alumiinilevyn välillä, havaitsemme hetkeä, jolloin kuvaajan kaltevuus lakkaa olemasta suoraviivainen ja leikkaa kaikki arvot yli tämä kohta pitää vain kohdat, joissa alumiinilevyn ja ympäristön välillä oli vähän lämmönvaihtoa.
Käytämme sitten yhtälöä W = (mc * ΔT) / t1 levylle vastaanotetun aurinkovoiman laskemiseksi. Jos jaamme aurinkoenergian, joka vastaanotetaan tämän voiman saaneen alumiinilevyn pintaan, saadaan yhtälön I = W / m ^ 2 mukaan auringon vastaanottama aurinkovoimakkuus.
Mittaa sitten maa-aurinkoetäisyyden ja auringon säteen (Rs / r) välinen suhde. Tätä varten projisoimme aurinkokuvan ruudulla ympyräpiirustuksella. Projisoimme kuvan niin, että se on täydellisesti ympyrän keskellä, ja sitten laskemme sekuntien lukumäärän ennen kuin aurinkokuva on kokonaan ympyrän ulkopuolella. Tietäen, että maapallosta nähty aurinko kulkee 360 astetta ympäri maata 24 tunnissa, laskemme kuinka paljon aurinko kulkee t sekunnissa.
Kaavion mukaan tan 〖(θ / 2) = (Rs / r)〗 pystymme laskemaan (Rs / r) käyttämällä tätä yhtälöä.
Yhtälöllä I = σ * (Rs / r) ^ 2 * 〖T_s〗 ^ 4, missä σ edustaa Stefan-Boltzmann-vakioita, R_s / r edustaa maapallon-aurinkoetäisyyden ja auringon säteen välistä suhdetta ja T_s edustaa auringon lämpötilaa, pystymme laskemaan auringon lämpötilan aiemmin laskettujen arvojen perusteella kirjoittamalla yhtälön arvoksi T_s = ∜ (I / (σ * 〖tan (θ / 2)〗 ^ 2)) .
On muistettava, että menetelmämme ei ota huomioon maan ilmakehän, joka estää 30–40% auringonsäteistä leveysasteellamme. Tämä tarkoittaa, että löytämämme arvojen tulisi olla alhaisemmat kuin auringon lämpötilan teoreettinen arvo. Joten teemme kaksi laskelmaa, laskelman, jossa ei oteta huomioon ilmakehää, ja laskelman, joka otetaan huomioon jakamalla kokeellisen intensiteetin arvo sädekappaleen prosenttimäärällä teoreettisella ilmakehällä, joka on 35 %.
keskustelu
Kokeelle 1 saadut arvot ovat 4993 ° K oikaistamattomana arvona ja 6492 ° K oikaistuna arvona. Jos verrataan näitä kahta arvoa teoreettisesti hyväksytyyn teoreettiseen arvoon 5778 ° K, saadaan prosentuaaliset erot -13,6% oikaistamattomalle ja 12,3% oikaistulle arvolle. Nämä arvot eivät ole kovin kaukana teoreettisesta arvosta käytetyn alkeellisen menetelmän kannalta. En kuitenkaan usko, että tämä essee tuottaa hyviä tuloksia. Menetelmämme virheiden syiden, joista keskustellaan myöhemmin tässä keskustelussa, pitäisi johtaa meidät teoreettista arvoa alempiin arvoihin. Koe-auringon lämpötila-arvo on kuitenkin säädetty ja korkeampi kuin teoreettinen arvo. Todennäköisin syy on, että levy ei ollut lämpötilatasapainossa ympäristön kanssa kokeen alussa, joten lämpötilaero olisi suurempi ja antaisi siten korkeamman auringon lämpötila-arvon kuin ennakoida. Tätä voidaan tukea sillä, että testin 1 aika-lämpötila-kuvaajassa arvojen lineaarisuus katkeaa hyvin varhaisessa vaiheessa kuvaaen, että levy on alkanut vaihtaa lämpöä ympäristössä. Tämä lineaarisuuskatko syntyy paljon aikaisemmin kuin vastaavassa kuvaajassa testille 2, jossa arvot pysyivät lineaarisina koko kuvaajan suhteen, mikä osoittaa, että levy ei ollut vielä alkanut tehdä lämpötilanvaihtoa.
Une fille est un paria, principalement de son propre fait, se refait une beauté, baise un mec au hasard qui lui glisse son extase, par naïveté, finit par être payé pour avoir des relations sexuelles avec un sale bâtard, commence à voir et baiser régulièrement un type extase et sortir avec lui, papa est licencié et commence à la violer, les garçons à l'école découvrent le problème de la prostitution, le chantage et la violent, maman découvre que papa l'a violée et la blâme et la met à la porte, vit avec son petit ami et paye ses habitudes de drogue et son style de vie en Des trafiquants de drogue assez routiniers deviennent prostitués à part entière. Ils subissent un avortement. Peu à peu, ils se transforment en un véritable type de marcheur ambulant, de l’argent est volé. Un petit ami louche la jette à la porte, elle se fait prendre par des sans-abri elle est à nouveau enceinte, dit qu'elle va changer sa vie pour le bébé, économise de l'argent dans la prise en charge de la prostitution, redevient toxicomane, trouve de l'argent, prend de l'argent, la prend, un groupe d'enfants la trouve et la frappe peut-être à misca rrying et prendre son argent, alors elle surdose d'héroïne et meurt. Là, sauvé vous survoler comme 225 pages.
Молодой парень хотел выглядеть круто со своим другом, поэтому он решил начать курить сигареты и незаконно купить alchool.
Сначала это было немного забавно, и его цель произвести впечатление на своего друга была достигнута, однако шутка утихла через несколько недель, и мы больше думали о его новом «крутом» привычке.
Чтобы вернуть их внимание, он решил пойти дальше, выкуривая больше сигарет в день, выпивая более крепкую школу. Он даже начал принимать наркотики.
Тем не менее, его друг стал очень быстрым и больше не обращал внимания на его потребление.
Он продолжал потреблять, хотя это было не потому, что он хотел выглядеть круто, он знал, что это больше не работает, ему просто это нравилось. Его предупреждали, его предупреждали, он не мог поверить, что его поймали с крючка.
Чем больше он потреблял, тем тяжелее становилось его вещество. Он больше не был давним другом, но он был одним из самых серьезных, и одним из самых важных, и одним из самых важных.
Он продолжал сближаться с новыми людьми, которых он заводил, тем глубже он погружался во тьму преступлений.
Прежде чем он знал это, он совершал серьезное преступление. То, что он делал, не могло быть классным подростком, теперь он преступник.
Он наркоман, он проститутка, он совершает воровство, он виновен в контрабанде, он подстрекает других к участию в преступлениях.
Он наконец понял, как изменить свою жизнь, но это было уже невозможно.
Он был слишком зависим от наркотиков, алкоголя и сигарет, чтобы остановить это. И слишком много людей зависели от его преступления, если он попытался остановить.
Он закончил с остальной частью своего дня, который он ожидал от него.
Сначала это было немного забавно, и его цель произвести впечатление на своего друга была достигнута, однако шутка утихла через несколько недель, и мы больше думали о его новом «крутом» привычке.
Чтобы вернуть их внимание, он решил пойти дальше, выкуривая больше сигарет в день, выпивая более крепкую школу. Он даже начал принимать наркотики.
Тем не менее, его друг стал очень быстрым и больше не обращал внимания на его потребление.
Он продолжал потреблять, хотя это было не потому, что он хотел выглядеть круто, он знал, что это больше не работает, ему просто это нравилось. Его предупреждали, его предупреждали, он не мог поверить, что его поймали с крючка.
Чем больше он потреблял, тем тяжелее становилось его вещество. Он больше не был давним другом, но он был одним из самых серьезных, и одним из самых важных, и одним из самых важных.
Он продолжал сближаться с новыми людьми, которых он заводил, тем глубже он погружался во тьму преступлений.
Прежде чем он знал это, он совершал серьезное преступление. То, что он делал, не могло быть классным подростком, теперь он преступник.
Он наркоман, он проститутка, он совершает воровство, он виновен в контрабанде, он подстрекает других к участию в преступлениях.
Он наконец понял, как изменить свою жизнь, но это было уже невозможно.
Он был слишком зависим от наркотиков, алкоголя и сигарет, чтобы остановить это. И слишком много людей зависели от его преступления, если он попытался остановить.
Он закончил с остальной частью своего дня, который он ожидал от него.
(this is gonna be so stereotypical .. .. i'm sorry Sam)
(This is gonna be so stereotypical i'm sorry)
Hey eh do eh you eh wanna eh play eh some eh osu eh? The eh polar eh bears eh are eh kinda eh messing eh with eh our eh trees eh my eh lucky eh axe eh is eh missing.
(I'M SORRY OKAY)
samX500 wrote:
Молодой парень хотел выглядеть круто со своим другом, поэтому он решил начать курить сигареты и незаконно купить alchool.
Сначала это было немного забавно, и его цель произвести впечатление на своего друга была достигнута, однако шутка утихла через несколько недель, и мы больше думали о его новом «крутом» привычке.
Чтобы вернуть их внимание, он решил пойти дальше, выкуривая больше сигарет в день, выпивая более крепкую школу. Он даже начал принимать наркотики.
Тем не менее, его друг стал очень быстрым и больше не обращал внимания на его потребление.
Он продолжал потреблять, хотя это было не потому, что он хотел выглядеть круто, он знал, что это больше не работает, ему просто это нравилось. Его предупреждали, его предупреждали, он не мог поверить, что его поймали с крючка.
Чем больше он потреблял, тем тяжелее становилось его вещество. Он больше не был давним другом, но он был одним из самых серьезных, и одним из самых важных, и одним из самых важных.
Он продолжал сближаться с новыми людьми, которых он заводил, тем глубже он погружался во тьму преступлений.
Прежде чем он знал это, он совершал серьезное преступление. То, что он делал, не могло быть классным подростком, теперь он преступник.
Он наркоман, он проститутка, он совершает воровство, он виновен в контрабанде, он подстрекает других к участию в преступлениях.
Он наконец понял, как изменить свою жизнь, но это было уже невозможно.
Он был слишком зависим от наркотиков, алкоголя и сигарет, чтобы остановить это. И слишком много людей зависели от его преступления, если он попытался остановить.
Он закончил с остальной частью своего дня, который он ожидал от него.
(This is gonna be so stereotypical i'm sorry)
Hey eh do eh you eh wanna eh play eh some eh osu eh? The eh polar eh bears eh are eh kinda eh messing eh with eh our eh trees eh my eh lucky eh axe eh is eh missing.
(I'M SORRY OKAY)
The birds ... flying ... are loved by God ... at least
the birds that fly are loved by God, not less. don't be sad ... oh praise the lord
kill me now...
the birds that fly are loved by God, not less. don't be sad ... oh praise the lord
kill me now...
A humiliating thread when you have to write under the Americans. Heh.
чертовски американцы да
