The main idea is to introduce mod multipliers. You can adjust the difficulty of EZ/HR/HT/DT mod. Higher mod multipliers make the effect of the mods more notable. By default, EZ, HR, HT, DT would have multipliers 1.0x. I suppose the multiplier to cap at 10x, but reserve the possibility to scale it over 10x.
Let's talk about DT first. Currently, DT makes the speed of the gameplay 50% higher, with mod multiplier at 10x, it would become 500% higher maximally. But what about the score? Faster speed ought to lead to higher score, but as the speed increases, the bonus score should increase slower and slower. I think using the arctan function is a good idea here:
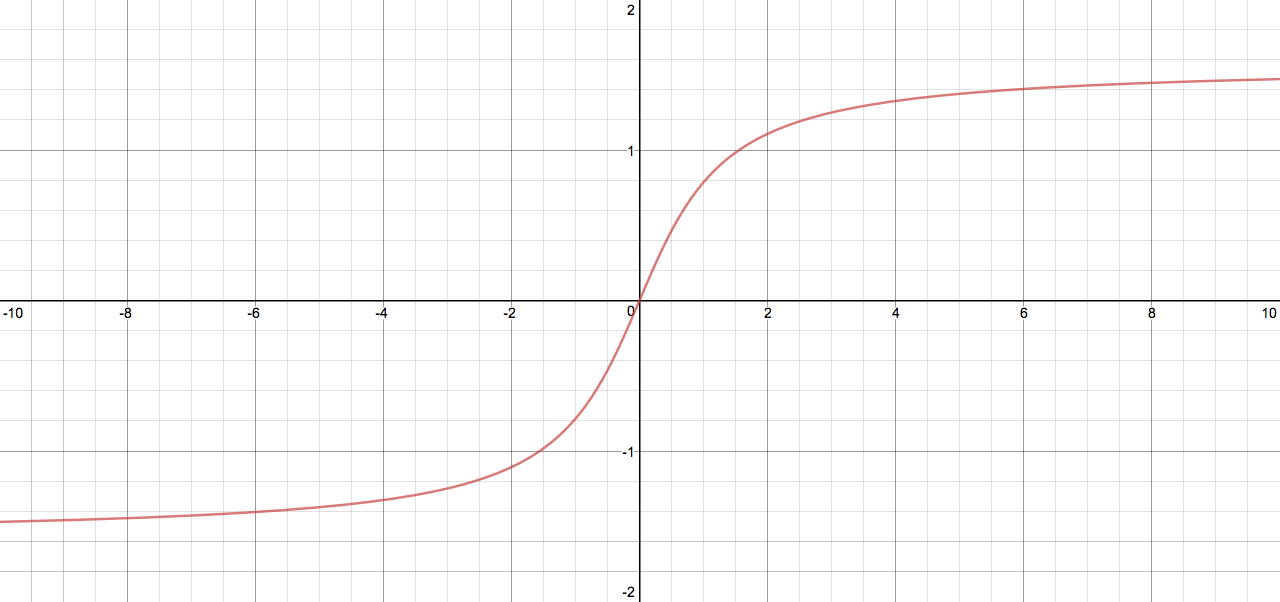
Now there are 2 requirements I want to fulfill:
1. When the mod multiplier is 1.0x, the score multiplier should be 1.12x.
2. When the mod multiplier is almost infinity, the score multiplier should be 1.24x.
And I'm going to scale the function linearly. I got this function:
The x-axis is the mod multiplier, and the y-axis is the score multiplier.
If you click the link above, you can see the formula I use on the left hand side.
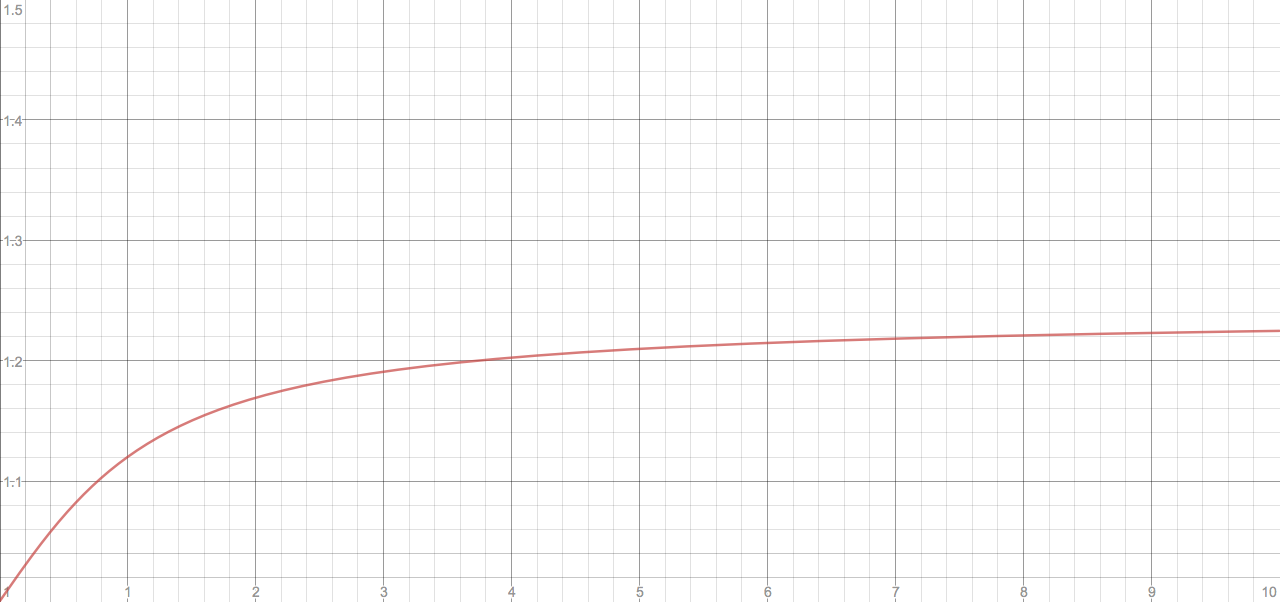
When it comes to HR, we can just set the CS multiplier to 1+0.3*(mod multiplier), and AR/HP/OD to 1+0.4*(mod multiplier), all of which multiplied with the original value capped at 10. I'm going to use the same strategy, that is, when the mod multiplier is 1.0x, the score multiplier should be 1.06x, and when the mod multiplier is almost infinity, the score multiplier should be 1.12x. Here's the graph:

There are also those (arguably) difficulty-reducing mods, namely EZ and HT. EZ would multiply CS/AR/HP/OD with 1/(1+(mod multiplier)), and we can do the same thing as HR to the score multiplier for EZ:
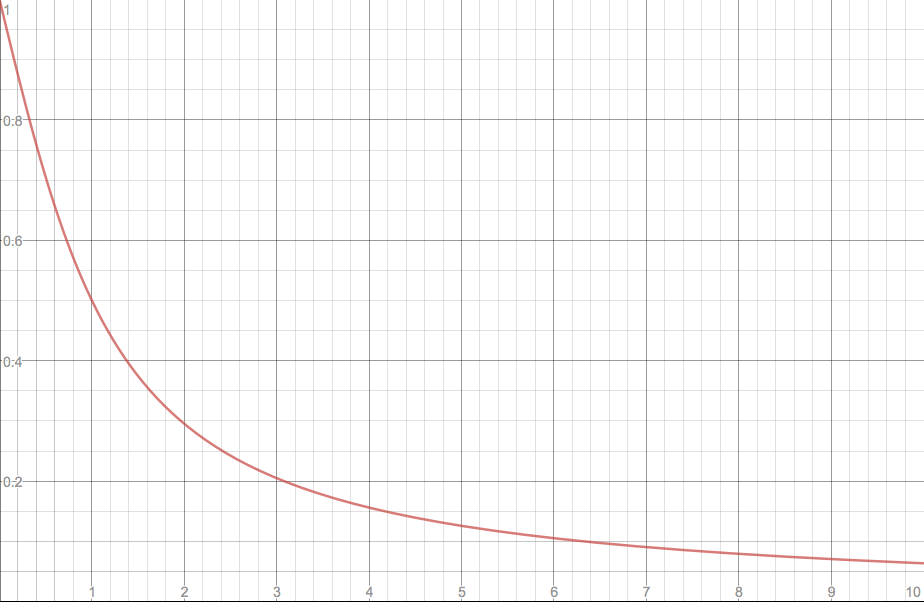
For HT, we can multiply the speed with 1/(1+(mod multiiplier/3)). Unfortunately, the score multiplier would quickly become negative, I suggest simply to make them unrankable when the mod multiplier is over 2:

Let's talk about DT first. Currently, DT makes the speed of the gameplay 50% higher, with mod multiplier at 10x, it would become 500% higher maximally. But what about the score? Faster speed ought to lead to higher score, but as the speed increases, the bonus score should increase slower and slower. I think using the arctan function is a good idea here:
Now there are 2 requirements I want to fulfill:
1. When the mod multiplier is 1.0x, the score multiplier should be 1.12x.
2. When the mod multiplier is almost infinity, the score multiplier should be 1.24x.
And I'm going to scale the function linearly. I got this function:
The x-axis is the mod multiplier, and the y-axis is the score multiplier.
If you click the link above, you can see the formula I use on the left hand side.
When it comes to HR, we can just set the CS multiplier to 1+0.3*(mod multiplier), and AR/HP/OD to 1+0.4*(mod multiplier), all of which multiplied with the original value capped at 10. I'm going to use the same strategy, that is, when the mod multiplier is 1.0x, the score multiplier should be 1.06x, and when the mod multiplier is almost infinity, the score multiplier should be 1.12x. Here's the graph:
There are also those (arguably) difficulty-reducing mods, namely EZ and HT. EZ would multiply CS/AR/HP/OD with 1/(1+(mod multiplier)), and we can do the same thing as HR to the score multiplier for EZ:
For HT, we can multiply the speed with 1/(1+(mod multiiplier/3)). Unfortunately, the score multiplier would quickly become negative, I suggest simply to make them unrankable when the mod multiplier is over 2: