Hey. So, there's information regarding OD, but there doesn't seem to be any for HP.
I'm about to change that.
HP difficulty is an often overlooked aspect of mapping - often there's a lot of feeling and guesswork involving what the optimal value is, so no particularily rational choices can be made about it. This post intends to explain how HP difficulty affects your maps.
After performing some testing, I have come to a few conclusions.
A single audio file of about 20 seconds consisting of silence was used. HP was set to each of the integer values from 0 to 10. By adding or removing a number of notes at a time, the number of notes required to fail was written for every HP value from 0 to 10. Once the number of notes to fill and to fail were known, two extra tests were performed. A test for a cap of a gain-per-second and a loss-per-second, and a test of whether the gain or loss is affected by the amount of health already had.
The following map was, in the end, constructed.
https://lunar.s-ul.eu/A0GU0VbT
Every difficulty is separated into a loss section, silence, and a gain section. Once the loss was figured out by not playing, there is a time of silence, and a bunch of notes meant to be autoplayed.

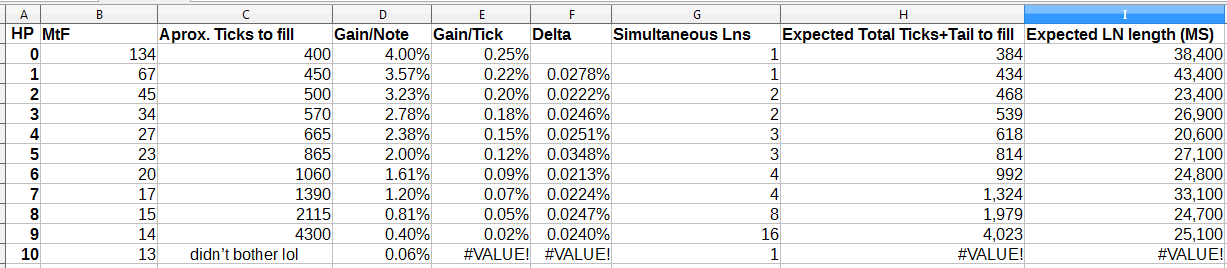
You can see the main results here. Everything onward is based off this table.
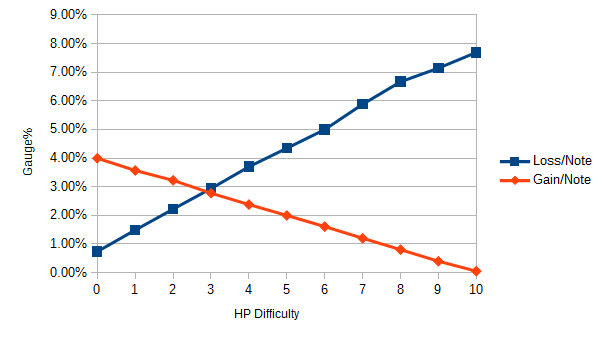
You can see both have a linear behaviour. Though, compounded, you will see in the next section what this actually causes.
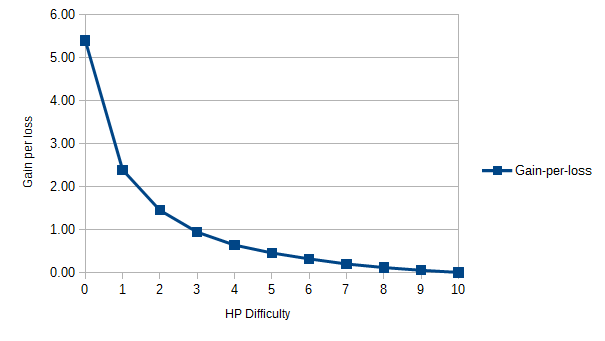
How many notes does one require to compensate for a loss? This is the last column, calculated by using the results of the Gain/Note column divided by the Loss/Note column. You can see the consequences of this setup. This is by far the most useful to know, since by the use of estimations you can get a very accurate gain-to-loss ratio for fine tuning your map. The value you see is how many notes you have to miss for a note to refill that loss.
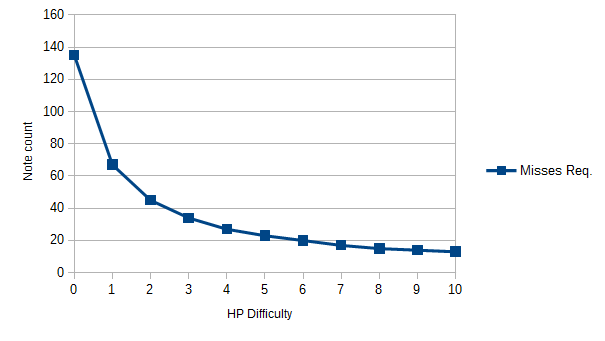
If there's another interpretation that can be useful for you as mappers, is the amount of notes you can miss in a row before failure. These are the charts seen after testing.
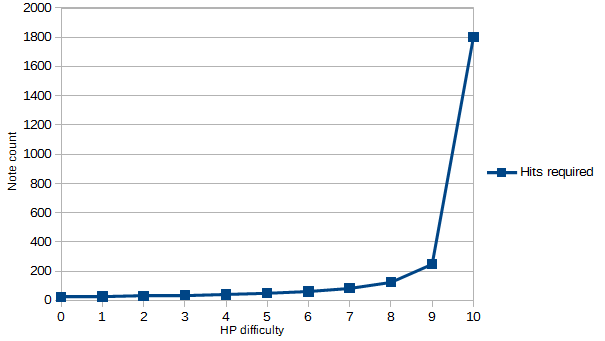
On the other hand, here are the hits to fill:
I hope this is useful. The best way to use this, in order to be precise, would be to perform a calculation of the ratio you desire. After running some linear regressions, the results are as follow:
LossPerNote(HP) = 0.71 * HP + 0.81
GainPerNote(HP) = -0.4 * HP + 3.98
In addition,
1 / LossPerNote(HP) = NotesToFail
1 / GainPerNote(HP) = NotesToFill
To find your desired target of Gain-to-loss, some more math is in order.
Gain-to-loss = GainPerNote(HP) / LossPerNote(HP)
Skipping to the results,
where R = Gain-to-Loss
HP = (0.81*R - 3.98) / (-0.4 - 0.71*R)
So, on the other hand, long notes are messed up.
Mechanically, the following happens:
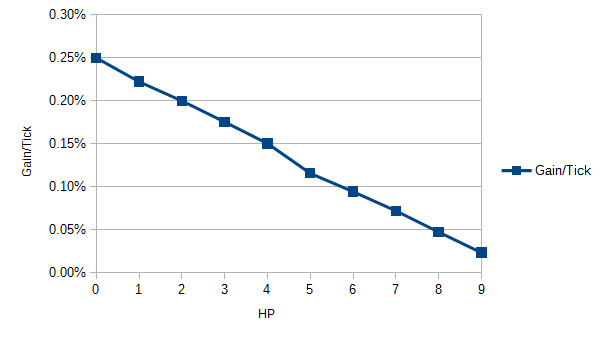
Gain/tick looks like this:
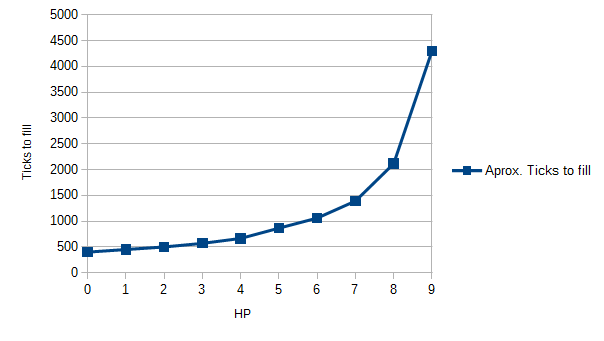
Ticks to fill looks like this (this is what I'm based off to say stuff above HP6 is harsh)
GainPerTick(HP) = -0.03 * HP + 0.25
The following information is provided by Blocko, by the following post: https://osu.ppy.sh/community/forums/posts/7201817
So I've been tweaking the equation for LossPerNote(HP) and GainPerNote(HP) based on the data Agka received since both equations are almost accurate to the table, but not quite.
After 30 minutes of tweaking, I came up with this equation that is as close to the table as possible. Here are the results:
LossPerNote(HP) = 0.75 * HP + 0.75
GainPerNote(HP) = -0.4 * HP + 4
To prevent GainPerNote(HP) from dividing by 0 once HP reaches 10, I changed that equation a bit more once HP reaches 9:
GainPerNote(HP) = -0.4 * (HP + ((HP - 9) / 180)) + 4
All of this is done to make the results for NotesToFail and NotesToFill match the data as close as possible. I hope this helps for people who want to do some numbers out there for their maps!
I'm about to change that.
Abstract
HP difficulty is an often overlooked aspect of mapping - often there's a lot of feeling and guesswork involving what the optimal value is, so no particularily rational choices can be made about it. This post intends to explain how HP difficulty affects your maps.
After performing some testing, I have come to a few conclusions.
- There's a linear increase of loss per note, and a linear decrease of gain per note.
- There are no caps for health change per unit of time.
- HP 0 and HP10 are absolutely ridiculous.
- There's an hyperbolic change on the gain-to-loss ratio as HP difficulty increases.
- After testing with Skalim, OD does not affect HP loss.
Testing method
A single audio file of about 20 seconds consisting of silence was used. HP was set to each of the integer values from 0 to 10. By adding or removing a number of notes at a time, the number of notes required to fail was written for every HP value from 0 to 10. Once the number of notes to fill and to fail were known, two extra tests were performed. A test for a cap of a gain-per-second and a loss-per-second, and a test of whether the gain or loss is affected by the amount of health already had.
The following map was, in the end, constructed.
https://lunar.s-ul.eu/A0GU0VbT
Every difficulty is separated into a loss section, silence, and a gain section. Once the loss was figured out by not playing, there is a time of silence, and a bunch of notes meant to be autoplayed.
Results
You can see the main results here. Everything onward is based off this table.
Gain and loss
You can see both have a linear behaviour. Though, compounded, you will see in the next section what this actually causes.
Gain-to-loss
How many notes does one require to compensate for a loss? This is the last column, calculated by using the results of the Gain/Note column divided by the Loss/Note column. You can see the consequences of this setup. This is by far the most useful to know, since by the use of estimations you can get a very accurate gain-to-loss ratio for fine tuning your map. The value you see is how many notes you have to miss for a note to refill that loss.
Misses to fail, hits to fill
If there's another interpretation that can be useful for you as mappers, is the amount of notes you can miss in a row before failure. These are the charts seen after testing.
On the other hand, here are the hits to fill:
I hope this is useful. The best way to use this, in order to be precise, would be to perform a calculation of the ratio you desire. After running some linear regressions, the results are as follow:
LossPerNote(HP) = 0.71 * HP + 0.81
GainPerNote(HP) = -0.4 * HP + 3.98
In addition,
1 / LossPerNote(HP) = NotesToFail
1 / GainPerNote(HP) = NotesToFill
To find your desired target of Gain-to-loss, some more math is in order.
Gain-to-loss = GainPerNote(HP) / LossPerNote(HP)
Skipping to the results,
where R = Gain-to-Loss
HP = (0.81*R - 3.98) / (-0.4 - 0.71*R)
Long Notes
So, on the other hand, long notes are messed up.
Mechanically, the following happens:
- Heads do not count for a miss.
- A head does not give health.
- Ticks and the tail give health. Tail gives same as a hit.
- A tick happens every 100ms. BPM, HP, Slider tickrate do not affect this.
- Anything above and including ~6HP is ridiculously harsh on pure LN maps.
- Gain/tick is linear. Just as gain/note.
- Ticks are triggered at the start of the time period (100ms)
- Hitting and releasing in the middle of the long note does not earn you a miss. Only missing the tail does.
Gain/tick looks like this:
Ticks to fill looks like this (this is what I'm based off to say stuff above HP6 is harsh)
GainPerTick(HP) = -0.03 * HP + 0.25
Blocko's addendum
The following information is provided by Blocko, by the following post: https://osu.ppy.sh/community/forums/posts/7201817
So I've been tweaking the equation for LossPerNote(HP) and GainPerNote(HP) based on the data Agka received since both equations are almost accurate to the table, but not quite.
After 30 minutes of tweaking, I came up with this equation that is as close to the table as possible. Here are the results:
LossPerNote(HP) = 0.75 * HP + 0.75
GainPerNote(HP) = -0.4 * HP + 4
To prevent GainPerNote(HP) from dividing by 0 once HP reaches 10, I changed that equation a bit more once HP reaches 9:
GainPerNote(HP) = -0.4 * (HP + ((HP - 9) / 180)) + 4
All of this is done to make the results for NotesToFail and NotesToFill match the data as close as possible. I hope this helps for people who want to do some numbers out there for their maps!
